Gaz idealny, równanie stanu gazu doskonałego, jego temperatura i ciśnienie, objętość… Lista parametrów i definicji używanych w odpowiednim dziale fizyki może być kontynuowana przez dość długi czas. Dzisiaj porozmawiamy właśnie na ten temat.
Co jest brane pod uwagę w fizyce molekularnej?

Głównym obiektem rozważanym w tej sekcji jest gaz doskonały. Przy uwzględnieniu normalnych warunków środowiskowych uzyskano równanie stanu gazu doskonałego, o czym porozmawiamy nieco później. Teraz podejdźmy do tego „problemu” z daleka.
Powiedzmy, że mamy pewną masę gazu. Jej stan można określić za pomocą trzech parametrów o charakterze termodynamicznym. Są to oczywiście ciśnienie, objętość i temperatura. Równanie stanu układu w tym przypadku będzie wzorem na związek między odpowiednimi parametrami. Wygląda to tak: F (p, V, T)=0.
Tu po raz pierwszy powoli zbliżamy się do pojawienia się czegoś takiego jak ideałgaz. Nazywa się to gazem, w którym interakcje między cząsteczkami są znikome. Ogólnie rzecz biorąc, nie istnieje w naturze. Jednak każdy wysoko rozrzedzony gaz jest mu bliski. Azot, tlen i powietrze, które występują w normalnych warunkach, niewiele różnią się od ideału. Aby napisać równanie stanu gazu doskonałego, możemy użyć zunifikowanego prawa gazu. Otrzymujemy: pV/T=const.
Podobna koncepcja nr 1: Prawo Avogadro
Może nam powiedzieć, że jeśli weźmiemy taką samą liczbę moli absolutnie dowolnego przypadkowego gazu i umieścimy je w tych samych warunkach, łącznie z temperaturą i ciśnieniem, to gazy zajmą tę samą objętość. W szczególności eksperyment przeprowadzono w normalnych warunkach. Oznacza to, że temperatura wynosiła 273,15 Kelwina, ciśnienie jednej atmosfery (760 milimetrów słupa rtęci lub 101325 paskali). Przy tych parametrach gaz zajmował objętość równą 22,4 litra. Można więc powiedzieć, że dla jednego mola dowolnego gazu stosunek parametrów liczbowych będzie wartością stałą. Dlatego postanowiono oznaczyć tę liczbę literą R i nazwać ją uniwersalną stałą gazową. Zatem równa się 8,31. Jednostką jest J/molK.
Gaz idealny. Równanie stanu gazu doskonałego i jego manipulacja
Spróbujmy przepisać formułę. Aby to zrobić, piszemy to w tej formie: pV=RT. Następnie wykonujemy prostą czynność, mnożąc obie strony równania przez dowolną liczbę moli. Otrzymujemy pVu=uRT. Weźmy pod uwagę fakt, że iloczyn objętości molowej iilość materii to po prostu objętość. Ale w końcu liczba moli będzie jednocześnie równa ilorazowi masy i masy molowej. Dokładnie tak wygląda równanie Mendelejewa-Clapeyrona. Daje jasne wyobrażenie o tym, jaki system tworzy gaz idealny. Równanie stanu gazu doskonałego przyjmie postać: pV=mRT/M.
Wyprowadź wzór na ciśnienie
Zróbmy więcej manipulacji z otrzymanymi wyrażeniami. Aby to zrobić, prawa strona równania Mendelejewa-Clapeyrona jest mnożona i dzielona przez liczbę Avogadro. Teraz uważnie przyjrzymy się iloczynowi ilości substancji przez liczbę Avogadro. To nic innego jak całkowita liczba cząsteczek w gazie. Ale jednocześnie stosunek uniwersalnej stałej gazowej do liczby Avogadro będzie równy stałej Boltzmanna. Dlatego też wzory na ciśnienie można zapisać następująco: p=NkT/V lub p=nkT. Tutaj symbol n oznacza stężenie cząstek.
Idealne procesy gazowe
W fizyce molekularnej istnieje coś takiego jak izoprocesy. Są to procesy termodynamiczne, które zachodzą w układzie przy jednym ze stałych parametrów. W takim przypadku masa substancji również musi pozostać stała. Przyjrzyjmy się im dokładniej. A więc prawa gazu doskonałego.
Ciśnienie pozostaje stałe
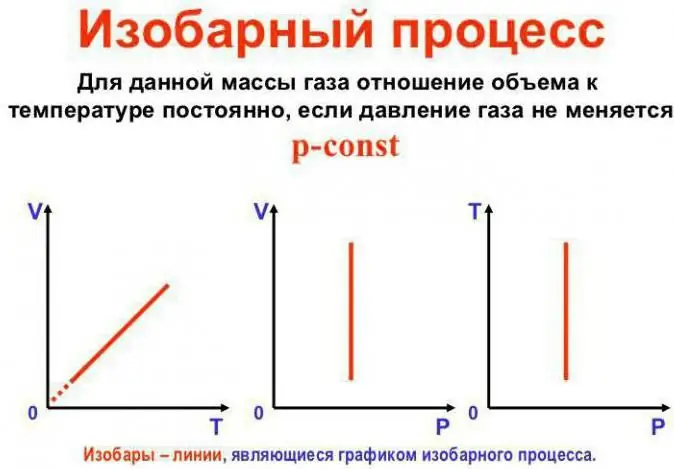
To jest prawo Gay-Lussaca. Wygląda to tak: V/T=const. Można to przepisać w inny sposób: V=Vo (1 + at). Tutaj a jest równe 1/273,15 K^-1 i jest nazywane „współczynnikiem rozszerzalności objętości”. Możemy podstawić temperaturę zarówno w stopniach Celsjusza, jak iskali Kelvina. W tym drugim przypadku otrzymujemy wzór V=Voat.
Głośność pozostaje stała

To drugie prawo Gay-Lussaca, częściej określane jako prawo Karola. Wygląda to tak: p/T=const. Jest jeszcze jedno sformułowanie: p=po (1 + at). Transformacje można przeprowadzić zgodnie z poprzednim przykładem. Jak widać, prawa gazu doskonałego są czasami dość do siebie podobne.
Temperatura pozostaje stała

Jeśli temperatura gazu doskonałego pozostaje stała, możemy otrzymać prawo Boyle-Mariotte. Można to zapisać tak: pV=const.
Powiązana koncepcja 2: Ciśnienie częściowe
Powiedzmy, że mamy statek z gazami. To będzie mieszanka. System znajduje się w stanie równowagi termicznej, a same gazy nie reagują ze sobą. Tutaj N oznacza całkowitą liczbę cząsteczek. N1, N2 itd., odpowiednio, liczba cząsteczek w każdym ze składników mieszaniny. Weźmy wzór na ciśnienie p=nkT=NkT/V. Można go otworzyć w konkretnym przypadku. Dla mieszaniny dwuskładnikowej wzór przyjmie postać: p=(N1 + N2) kT/V. Ale potem okazuje się, że ciśnienie całkowite zostanie zsumowane z ciśnień cząstkowych każdej mieszaniny. Tak więc będzie wyglądać jak p1 + p2 i tak dalej. Będą to ciśnienia cząstkowe.
Do czego to służy?
Otrzymany przez nas wzór wskazuje, że ciśnienie w układzie pochodzi z każdej grupy cząsteczek. Nawiasem mówiąc, to nie zależy odinni. D alton wykorzystał to, formułując prawo, nazwane później jego imieniem: w mieszaninie, w której gazy nie reagują ze sobą chemicznie, całkowite ciśnienie będzie równe sumie ciśnień cząstkowych.






