Każda osoba w swoim życiu napotyka ciała znajdujące się w jednym z trzech zbiorczych stanów materii. Najprostszym stanem skupienia do zbadania jest gaz. W artykule rozważymy pojęcie gazu doskonałego, podamy równanie stanu układu, a także zwrócimy uwagę na opis temperatury bezwzględnej.
Stan gazu
Każdy uczeń ma dobre pojęcie o stanie materii, o którym mówi, gdy słyszy słowo „gaz”. Słowo to rozumiane jest jako ciało, które jest w stanie zajmować dowolną dostarczoną mu objętość. Nie jest w stanie zachować swojego kształtu, ponieważ nie jest w stanie oprzeć się nawet najdrobniejszemu wpływowi zewnętrznemu. Ponadto gaz nie zatrzymuje objętości, co odróżnia go nie tylko od ciał stałych, ale także od cieczy.
Podobnie jak ciecz, gaz jest substancją płynną. W procesie ruchu ciał stałych w gazach te ostatnie utrudniają ten ruch. Powstała siła nazywana jest oporem. Jego wartość zależy odprędkość ciała w gazie.
Dobrymi przykładami gazów są powietrze, gaz ziemny używany do ogrzewania domów i gotowania, gazy obojętne (Ne, Ar) używane do wypełniania reklamowych rur żarowych lub używane do tworzenia obojętnego (nieagresywnego, ochronnego) środowiska podczas spawania.
Gaz idealny
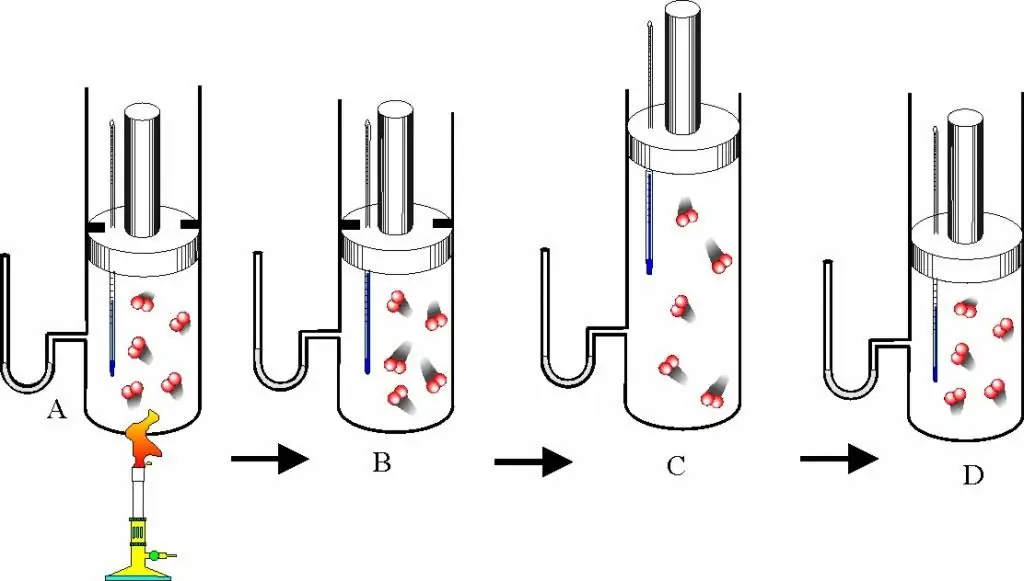
Zanim przejdziesz do opisu praw gazu i równania stanu, powinieneś dobrze zrozumieć pytanie, czym jest gaz doskonały. Koncepcja ta została wprowadzona do teorii kinetyki molekularnej (MKT). Gaz doskonały to każdy gaz, który spełnia następujące cechy:
- Cząstki, które go tworzą, nie oddziałują ze sobą, z wyjątkiem bezpośrednich zderzeń mechanicznych.
- W wyniku zderzenia cząstek ze ścianami naczynia lub między sobą, ich energia kinetyczna i pęd są zachowane, to znaczy zderzenie uważane jest za całkowicie sprężyste.
- Cząstki nie mają wymiarów, ale mają skończoną masę, to znaczy są podobne do punktów materialnych.
To naturalne, że każdy gaz nie jest idealny, ale prawdziwy. Niemniej jednak, dla rozwiązania wielu praktycznych problemów, przybliżenia te są całkiem słuszne i można je wykorzystać. Istnieje ogólna zasada empiryczna, która mówi: niezależnie od natury chemicznej, jeśli gaz ma temperaturę wyższą od temperatury pokojowej i ciśnienie rzędu atmosferycznego lub niższego, to z dużą dokładnością można go uznać za idealny i można go wykorzystać do opisu to.wzór równania stanu gazu doskonałego.
Prawo Clapeyrona-Mendeleeva
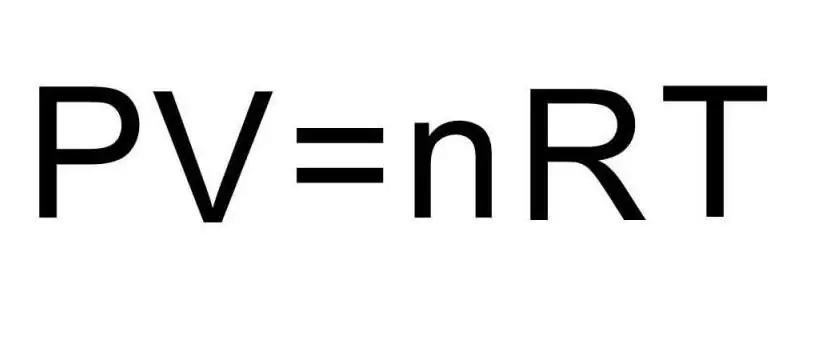
Przejściami między różnymi stanami skupienia materii i procesami w jednym stanie skupienia zajmuje się termodynamika. Ciśnienie, temperatura i objętość to trzy wielkości, które jednoznacznie definiują każdy stan układu termodynamicznego. Wzór na równanie stanu gazu doskonałego łączy wszystkie trzy wielkości w jedną równość. Napiszmy tę formułę:
PV=nRT
Tutaj P, V, T - odpowiednio ciśnienie, objętość, temperatura. Wartość n to ilość substancji w molach, a symbol R oznacza uniwersalną stałą gazów. Ta równość pokazuje, że im większy iloczyn ciśnienia i objętości, tym większy musi być iloczyn ilości substancji i temperatury.

Wzór na równanie stanu gazu nazywa się prawem Clapeyrona-Mendeleeva. W 1834 roku francuski naukowiec Emile Clapeyron, podsumowując eksperymentalne wyniki swoich poprzedników, doszedł do tego równania. Jednak Clapeyron zastosował szereg stałych, które później Mendelejew zastąpił jedną - uniwersalną stałą gazową R (8, 314 J / (molK)). Dlatego we współczesnej fizyce to równanie nosi imię francuskich i rosyjskich naukowców.

Inne formy równań
Powyżej napisaliśmy równanie stanu Mendelejewa-Clapeyrona dla gazu doskonałego w ogólnie przyjętym iwygodna forma. Jednak w problemach termodynamiki często może być wymagana nieco inna forma. Poniżej zapisano jeszcze trzy formuły, które bezpośrednio wynikają z zapisanego równania:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Te trzy równania są również uniwersalne dla gazu doskonałego, tylko w nich pojawiają się takie wielkości jak masa m, masa molowa M, gęstość ρ i liczba cząstek N tworzących układ. Symbol kB oznacza tutaj stałą Boltzmanna (1, 3810-23J/K).
Prawo Boyle-Mariotte
Kiedy Clapeyron sporządził swoje równanie, oparł się na prawach gazu, które zostały odkryte eksperymentalnie kilkadziesiąt lat wcześniej. Jednym z nich jest prawo Boyle-Mariotte. Odzwierciedla proces izotermiczny w układzie zamkniętym, w wyniku którego zmieniają się takie parametry makroskopowe jak ciśnienie i objętość. Jeśli w równaniu stanu gazu doskonałego umieścimy stałą T i n, to prawo gazu przyjmie postać:
P1V1=P2V 2
Jest to prawo Boyle-Mariotte, które mówi, że iloczyn ciśnienia i objętości jest zachowywany podczas dowolnego procesu izotermicznego. W tym przypadku zmieniają się same wartości P i V.
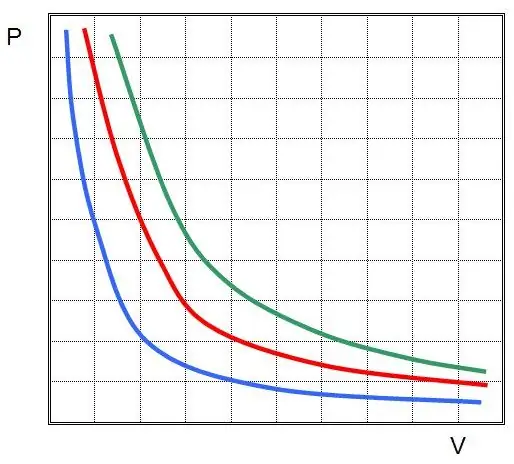
Jeśli wykreślisz P(V) lub V(P), to izotermy będą hiperbolami.
Prawa Karola i Gay-Lussaca
Te prawa matematycznie opisują izobarię i izochorycznośćprocesy, czyli takie przejścia między stanami układu gazowego, w których odpowiednio ciśnienie i objętość są zachowane. Prawo Karola można matematycznie zapisać w następujący sposób:
V/T=const, gdy n, P=const.
Prawo Gay-Lussaca jest napisane w następujący sposób:
P/T=const, gdy n, V=const.
Jeżeli obie równości zostaną przedstawione w postaci wykresu, to otrzymamy linie proste nachylone pod pewnym kątem do osi x. Ten typ wykresu wskazuje na bezpośrednią proporcjonalność między objętością a temperaturą przy stałym ciśnieniu oraz między ciśnieniem a temperaturą przy stałej objętości.
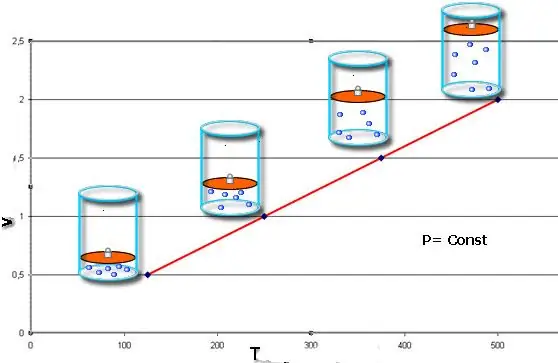
Zauważ, że wszystkie trzy rozważane prawa dotyczące gazu nie biorą pod uwagę składu chemicznego gazu, jak również zmiany w jego ilości materii.
Temperatura absolutna
W życiu codziennym jesteśmy przyzwyczajeni do używania skali temperatury Celsjusza, ponieważ jest ona wygodna do opisywania procesów wokół nas. Tak więc woda wrze w temperaturze 100 oC i zamarza w temperaturze 0 oC. W fizyce skala ta okazuje się niewygodna, dlatego stosuje się tak zwaną skalę temperatury absolutnej, która została wprowadzona przez Lorda Kelvina w połowie XIX wieku. Zgodnie z tą skalą temperatura jest mierzona w kelwinach (K).
Uważa się, że w temperaturze -273,15 oC nie występują drgania termiczne atomów i cząsteczek, ich ruch do przodu zatrzymuje się całkowicie. Ta temperatura w stopniach Celsjusza odpowiada zerowi bezwzględnemu w kelwinach (0 K). Z tej definicjifizyczne znaczenie temperatury absolutnej jest następujące: jest to miara energii kinetycznej cząstek tworzących materię, na przykład atomów lub cząsteczek.
Oprócz powyższego fizycznego znaczenia temperatury absolutnej, istnieją inne podejścia do zrozumienia tej wielkości. Jednym z nich jest wspomniane prawo gazowe Karola. Napiszmy to w następującej formie:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Ostatnia równość mówi, że przy określonej ilości substancji w układzie (na przykład 1 mol) i określonym ciśnieniu (na przykład 1 Pa), objętość gazu jednoznacznie określa temperaturę bezwzględną. Innymi słowy, wzrost objętości gazu w tych warunkach jest możliwy tylko ze względu na wzrost temperatury, a spadek objętości wskazuje na spadek wartości T.
Przypomnij sobie, że w przeciwieństwie do temperatury Celsjusza, temperatura bezwzględna nie może być ujemna.
Zasada Avogadro i mieszanki gazów
Oprócz powyższych praw gazu, równanie stanu gazu doskonałego prowadzi również do zasady odkrytej przez Amedeo Avogadro na początku XIX wieku, która nosi jego nazwisko. Zasada ta stanowi, że objętość dowolnego gazu przy stałym ciśnieniu i temperaturze zależy od ilości substancji w układzie. Odpowiednia formuła wygląda tak:
n/V=const, gdy P, T=const.
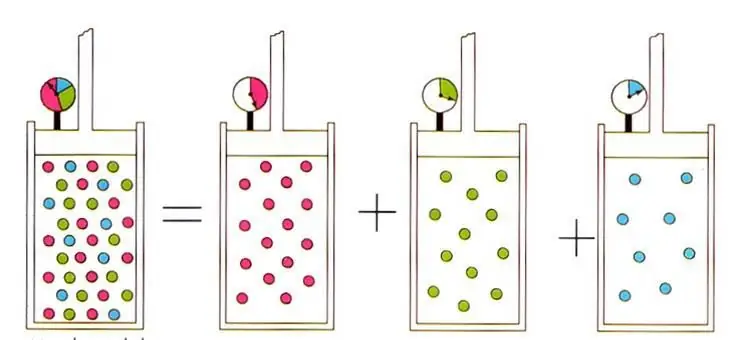
Wyrażenie pisemne prowadzi do dobrze znanego w fizyce gazu doskonałego prawa D altona dla mieszanin gazowych. Tenprawo stanowi, że ciśnienie cząstkowe gazu w mieszaninie jest jednoznacznie określone przez jego frakcję atomową.
Przykład rozwiązywania problemów
W zamkniętym naczyniu o sztywnych ściankach, zawierającym gaz doskonały, w wyniku ogrzewania ciśnienie wzrosło trzykrotnie. Konieczne jest określenie temperatury końcowej układu, jeśli jej wartość początkowa wynosiła 25 oC.
Najpierw przeliczmy temperaturę ze stopni Celsjusza na kelwiny, mamy:
T=25 + 273, 15=298, 15 K.
Ponieważ ściany naczynia są sztywne, proces ogrzewania można uznać za izochoryczny. W tym przypadku stosujemy prawo Gay-Lussaca, mamy:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
W ten sposób temperatura końcowa jest określana z iloczynu stosunku ciśnień i temperatury początkowej. Podstawiając dane do równości otrzymujemy odpowiedź: T2=894,45 K. Ta temperatura odpowiada 621,3 oC.






