Termodynamika skupienia gazowego stanu skupienia materii jest ważną gałęzią fizyki zajmującą się badaniem równowagi termodynamicznej i quasi-statycznych przejść w układach. Głównym modelem, na którym opierają się przewidywania zachowania systemów, jest model gazu doskonałego. Za jego pomocą uzyskano równanie Mendelejewa-Clapeyrona. Rozważ to w artykule.
Gaz idealny
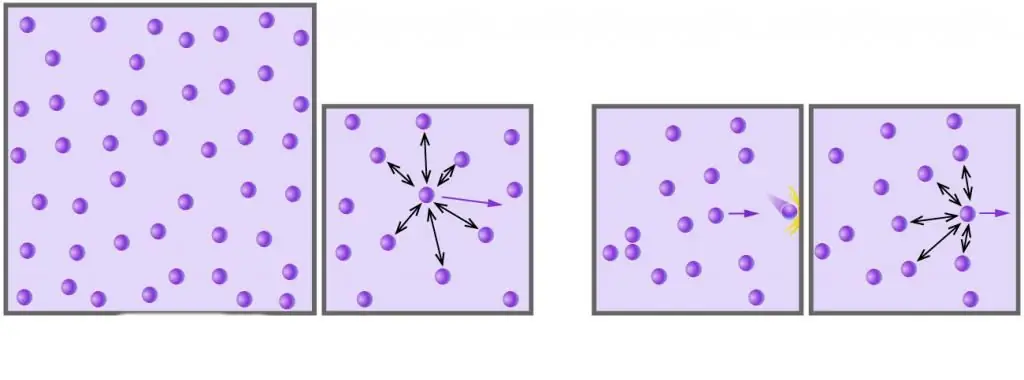
Jak wiesz, wszystkie gazy rzeczywiste składają się z cząsteczek lub atomów, których odległości są zbyt duże w porównaniu z ich rozmiarami przy niskim ciśnieniu. Ponadto w wysokich temperaturach, w skali bezwzględnej, energia kinetyczna cząsteczek przekracza ich energię potencjalną związaną ze słabymi oddziaływaniami dipol-dipol (jeśli oprócz tych oddziaływań istnieją inne rodzaje wiązań chemicznych, na przykład jonowe lub wodór, wtedy wnoszą znaczący wkład w potencjalny składnik energii układu wewnętrznego).
Ze względu naW przypadku wielu gazów rzeczywistych w warunkach zbliżonych do normalnych można pominąć ich interakcje wewnętrzne i rozmiary cząstek. Te dwa główne przybliżenia składają się na model gazu doskonałego.
Równanie Mendelejewa w fizyce

Bardziej poprawne i sprawiedliwe jest nazwanie tego równania prawem Clapeyrona-Mendeleeva. Faktem jest, że po raz pierwszy został nagrany przez francuskiego inżyniera Emile Clapeyrona w 1834 roku. Dokonał tego, analizując prawa gazowe Boyle-Mariotte, Gay-Lussaca i Charlesa odkryte na początku XIX wieku.
Zasługa rosyjskiego chemika Dmitrija Mendelejewa polega na tym, że nadał równaniu nowoczesną i łatwą w użyciu formę matematyczną. W szczególności Mendelejew wprowadził do równania stałą dla wszystkich gazów R=8,314 J/(molK). Sam Clapeyron użył wielu stałych empirycznych, które utrudniają proces obliczeniowy.
Równanie Mendelejewa-Clapeyrona jest zapisane w następujący sposób:
PV=nRT.
Ta równość oznacza, że iloczyn ciśnienia P i objętości V po lewej stronie wyrażenia jest zawsze proporcjonalny do iloczynu temperatury bezwzględnej T i ilości substancji n po lewej stronie.
Badane wyrażenie pozwala uzyskać dowolne prawo gazu, jeśli ustalisz dwa z czterech jego parametrów. W przypadku izoprocesów badane są układy zamknięte, w których nie zachodzi wymiana materii z otoczeniem (n=const). Procesy te charakteryzują się jednym stałym parametrem termodynamicznym (T, P lub V).

Przykładowy problem
Teraz rozwiążmy problem z równaniem Mendelejewa-Clapeyrona. Wiadomo, że tlen o wadze 500 gramów znajduje się w butli o pojemności 100 litrów pod ciśnieniem 2 atmosfer. Jaka jest temperatura w balonie, biorąc pod uwagę, że układ jest w równowadze termodynamicznej.
Przypomnijmy, że zgodnie z definicją ilość substancji oblicza się według wzoru:
n=m/M.
Gdzie m jest masą wszystkich cząstek układu, M jest ich średnią masą molową. Ta równość pozwala nam przepisać równanie Mendelejewa w następującej postaci:
PV=mRT/M.
Gdzie otrzymujemy działającą formułę dla tego zadania:
T=PVM/(mR).
Pozostaje przekonwertować wszystkie wielkości na jednostki SI i zastąpić je następującym wyrażeniem:
T=21013250, 10, 032/(0, 58, 314)=156 K.
Wyliczona temperatura wynosi -117 oC. Chociaż tlen w tej temperaturze jest nadal w postaci gazowej (kondensuje się w temperaturze -182,96 oC), w takich warunkach model gazu doskonałego może być użyty jedynie do uzyskania jakościowego oszacowania obliczonej wartości.






