Badanie procesów zachodzących w systemach statystycznych komplikuje minimalna wielkość cząstek i ich ogromna liczba. Praktycznie niemożliwe jest rozpatrywanie każdej cząstki osobno, dlatego wprowadzane są wielkości statystyczne: średnia prędkość cząstek, ich stężenie, masa cząstek. Wzór charakteryzujący stan układu z uwzględnieniem parametrów mikroskopowych nazywany jest podstawowym równaniem molekularno-kinetycznej teorii gazów (MKT).
Trochę o średniej prędkości cząstek
Wyznaczanie prędkości cząstek zostało po raz pierwszy przeprowadzone eksperymentalnie. Znany eksperyment z programu szkolnego, przeprowadzony przez Otto Sterna, pozwolił stworzyć ideę prędkości cząstek. W trakcie eksperymentu badano ruch atomów srebra w obracających się cylindrach: najpierw w stanie stacjonarnym instalacji, a następnie podczas obracania się z określoną prędkością kątową.
W rezultacie stwierdzono, że prędkość cząsteczek srebra przekracza prędkość dźwięku i wynosi 500 m/s. Fakt jest dość interesujący, ponieważ człowiekowi trudno jest wyczuć takie prędkości ruchu cząstek w substancjach.
Gaz idealny
Kontynuuj badaniaWydaje się to możliwe tylko w układzie, którego parametry można określić za pomocą bezpośrednich pomiarów za pomocą przyrządów fizycznych. Prędkość mierzy się prędkościomierzem, ale pomysł dołączenia prędkościomierza do pojedynczej cząstki jest absurdalny. Tylko makroskopowy parametr związany z ruchem cząstek może być bezpośrednio zmierzony.
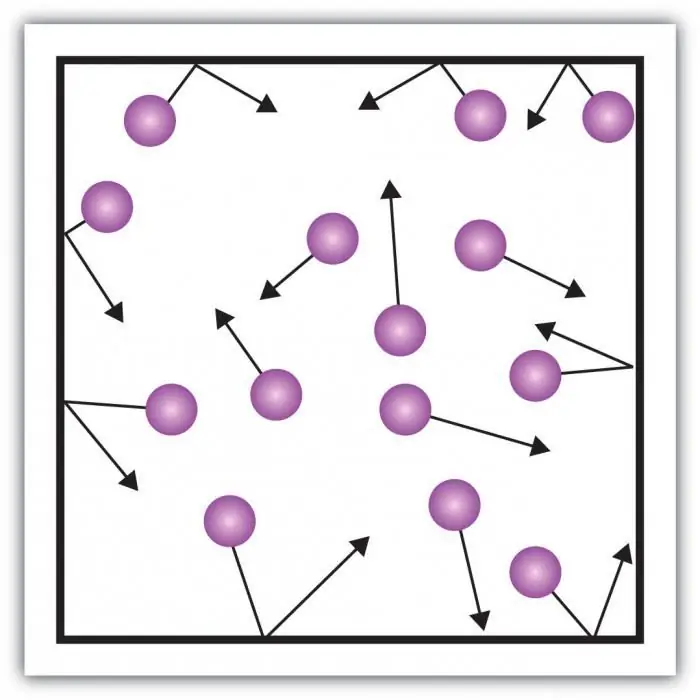
Rozważ ciśnienie gazu. Nacisk na ścianki naczynia jest wytwarzany przez uderzenia cząsteczek gazu w naczyniu. Osobliwością gazowego stanu materii są wystarczająco duże odległości między cząsteczkami i ich małe wzajemne oddziaływanie. Pozwala to bezpośrednio zmierzyć jego ciśnienie.
Każdy układ oddziałujących ze sobą ciał charakteryzuje energia potencjalna i energia kinetyczna ruchu. Prawdziwy gaz to złożony system. Zmienność energii potencjalnej nie poddaje się systematyzacji. Problem można rozwiązać, wprowadzając model, który przenosi charakterystyczne właściwości gazu, odrzucając złożoność interakcji.
Gaz idealny to stan materii, w którym oddziaływanie cząstek jest znikome, energia potencjalna oddziaływania dąży do zera. Tylko energia ruchu, która zależy od prędkości cząstek, może być uważana za znaczącą.
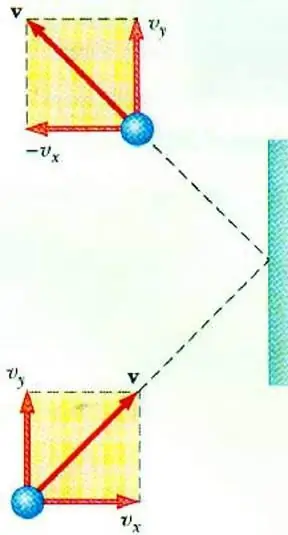
Idealne ciśnienie gazu
Odkrycie związku między ciśnieniem gazu a prędkością jego cząstek pozwala na podstawowe równanie MKT gazu doskonałego. Cząstka poruszająca się w naczyniu po zderzeniu ze ścianą przekazuje mu impuls, którego wartość można określić na podstawie drugiej zasadyNewton:
F∆t=2m0vx
Zmiana pędu cząstki podczas uderzenia sprężystego wiąże się ze zmianą składowej poziomej jej prędkości. F jest siłą działającą od strony cząstki na ścianę przez krótki czas t; m0 - masa cząstki.
Wszystkie cząstki gazu zderzają się z powierzchnią obszaru S w czasie ∆t, poruszając się w kierunku powierzchni z prędkością vx i znajdując się w cylindrze o objętości Sυ x Δt. Przy stężeniu cząstek n dokładnie połowa cząsteczek porusza się w kierunku ściany, druga połowa porusza się w przeciwnym kierunku.
Po rozważeniu zderzenia wszystkich cząstek, możemy napisać prawo Newtona dla siły działającej na powierzchnię:
F∆t=nm0vx2S∆t
Ponieważ ciśnienie gazu jest definiowane jako stosunek siły działającej prostopadle do powierzchni do powierzchni tej ostatniej, możemy napisać:
p=F: S=nm0vx2
Wynikowa relacja jako podstawowe równanie MKT nie może opisywać całego układu, ponieważ uwzględniany jest tylko jeden kierunek ruchu.
Dystrybucja Maxwella
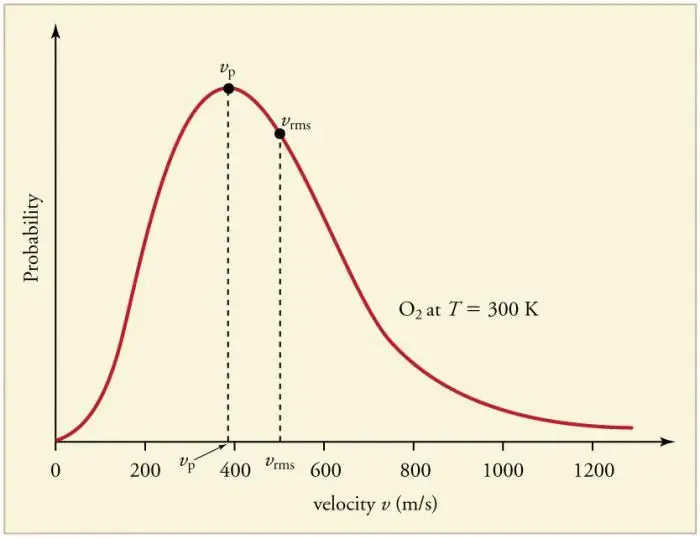
Częste zderzenia cząstek gazu ze ścianami i ze sobą nawzajem prowadzą do ustalenia pewnego statystycznego rozkładu cząstek pod względem prędkości (energii). Kierunki wszystkich wektorów prędkości okazują się jednakowo prawdopodobne. Ta dystrybucja nazywa się dystrybucją Maxwella. W 1860 r. ten wzór byłwyprowadzony przez J. Maxwella na podstawie MKT. Główne parametry prawa rozkładu nazywane są prędkościami: prawdopodobnymi, odpowiadającymi maksymalnej wartości krzywej, oraz wartością średnią kwadratową vkv=√‹v2 › - średni kwadrat prędkości cząstek.
Wzrost temperatury gazu odpowiada wzrostowi prędkości.
Na podstawie faktu, że wszystkie prędkości są równe, a ich moduły mają tę samą wartość, możemy założyć:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, od: ‹ vx2›=‹v2›: 3
Podstawowe równanie MKT, uwzględniające średnią wartość ciśnienia gazu, to:
p=nm0‹v2›: 3.
Ta zależność jest wyjątkowa, ponieważ określa związek między parametrami mikroskopowymi: prędkością, masą cząstek, stężeniem cząstek i ogólnie ciśnieniem gazu.
Korzystając z pojęcia energii kinetycznej cząstek, podstawowe równanie MKT można zapisać inaczej:
p=2nm0‹v2›: 6=2n‹Ek›: 3
Ciśnienie gazu jest proporcjonalne do średniej wartości energii kinetycznej jego cząstek.
Temperatura
Co ciekawe, dla stałej ilości gazu w zamkniętym naczyniu można powiązać ciśnienie gazu i średnią wartość energii ruchu cząstek. W takim przypadku ciśnienie można zmierzyć, mierząc energięcząstki.
Co robić? Jaką wartość można porównać z energią kinetyczną? Taką wartością okazuje się temperatura.

Temperatura jest miarą stanu termicznego substancji. Do jego pomiaru stosuje się termometr, którego podstawą jest rozszerzalność cieplna płynu roboczego (alkoholu, rtęci) po podgrzaniu. Skala termometru jest tworzona eksperymentalnie. Zwykle umieszcza się na nim znaki odpowiadające położeniu płynu roboczego podczas pewnego procesu fizycznego zachodzącego w stałym stanie termicznym (wrząca woda, topniejący lód). Różne termometry mają różne skale. Na przykład stopnie Celsjusza, Fahrenheita.

Uniwersalna skala temperatury
Termometry gazowe można uznać za bardziej interesujące pod względem niezależności od właściwości płynu roboczego. Ich skala nie zależy od rodzaju używanego gazu. W takim urządzeniu można hipotetycznie wyodrębnić temperaturę, w której ciśnienie gazu dąży do zera. Obliczenia pokazują, że ta wartość odpowiada -273,15 oC. Skala temperatury (skala temperatury absolutnej lub skala Kelvina) została wprowadzona w 1848 roku. Za główny punkt tej skali przyjęto możliwą temperaturę zerowego ciśnienia gazu. Segment jednostki skali jest równy wartości jednostki skali Celsjusza. Wydaje się, że wygodniejsze jest zapisanie podstawowego równania MKT przy użyciu temperatury podczas badania procesów gazowych.
Zależność między ciśnieniem a temperaturą
Empirycznie możesz to zweryfikowaćproporcjonalność ciśnienia gazu do jego temperatury. Jednocześnie stwierdzono, że ciśnienie jest wprost proporcjonalne do stężenia cząstek:
P=nkT,
gdzie T jest temperaturą bezwzględną, k jest stałą równą 1,38•10-23J/K.
Podstawowa wartość, która ma stałą wartość dla wszystkich gazów, nazywana jest stałą Boltzmanna.
Porównując zależność ciśnienia od temperatury i podstawowe równanie gazów MKT, możemy napisać:
‹Ek›=3kT: 2
Średnia wartość energii kinetycznej ruchu cząsteczek gazu jest proporcjonalna do jego temperatury. Oznacza to, że temperatura może służyć jako miara energii kinetycznej ruchu cząstki.






