Podczas badania własności równania kwadratowego ustalono ograniczenie - dla dyskryminatora mniejszego od zera nie ma rozwiązania. Od razu zastrzeżono, że mówimy o zestawie liczb rzeczywistych. Dociekliwy umysł matematyka zainteresuje się - jaki jest sekret zawarty w klauzuli o rzeczywistych wartościach?
Z biegiem czasu matematycy wprowadzili koncepcję liczb zespolonych, w której warunkowa wartość drugiego pierwiastka minus jeden jest traktowana jako jednostka.
Tło historyczne
Teoria matematyczna rozwija się sekwencyjnie, od prostych do złożonych. Zastanówmy się, jak powstało pojęcie „liczby zespolonej” i dlaczego jest potrzebne.
Od niepamiętnych czasów podstawą matematyki była zwykła relacja. Badacze znali tylko naturalny zestaw wartości. Dodawanie i odejmowanie były proste. W miarę jak relacje ekonomiczne stawały się coraz bardziej złożone, zaczęto stosować mnożenie zamiast dodawania tych samych wartości. Istnieje odwrotna operacja, abymnożenie - dzielenie.
Koncepcja liczby naturalnej ograniczała użycie operacji arytmetycznych. Nie da się rozwiązać wszystkich problemów dzielenia na zbiorze wartości całkowitych. Praca z ułamkami doprowadziła najpierw do koncepcji wartości racjonalnych, a następnie do wartości irracjonalnych. Jeśli dla racjonalnego można wskazać dokładną lokalizację punktu na linii, to dla irracjonalnego nie można wskazać takiego punktu. Możesz tylko przybliżyć interwał. Połączenie liczb wymiernych i niewymiernych utworzyło zbiór rzeczywisty, który można przedstawić jako pewną linię o określonej skali. Każdy krok wzdłuż linii jest liczbą naturalną, a pomiędzy nimi znajdują się wartości wymierne i niewymierne.
Rozpoczęła się era matematyki teoretycznej. Rozwój astronomii, mechaniki, fizyki wymagał rozwiązywania coraz bardziej skomplikowanych równań. Ogólnie znaleziono pierwiastki równania kwadratowego. Podczas rozwiązywania bardziej złożonego wielomianu sześciennego naukowcy napotkali sprzeczność. Pojęcie pierwiastka sześciennego z liczby ujemnej ma sens, ale dla pierwiastka kwadratowego uzyskuje się niepewność. Co więcej, równanie kwadratowe jest tylko szczególnym przypadkiem równania sześciennego.
W 1545 r. Włoch J. Cardano zaproponował wprowadzenie koncepcji liczby urojonej.

Ta liczba jest drugim pierwiastkiem minus jeden. Pojęcie liczby zespolonej powstało ostatecznie dopiero trzysta lat później w pracach słynnego matematyka Gaussa. Zaproponował formalne rozszerzenie wszystkich praw algebry do liczby urojonej. Prawdziwa linia została przedłużona dosamoloty. Świat jest większy.
Podstawowe koncepcje
Przypomnij kilka funkcji, które mają ograniczenia w rzeczywistym zestawie:
- y=arcsin(x), zdefiniowany między ujemną a dodatnią 1.
- y=ln(x), logarytm dziesiętny ma sens z argumentami dodatnimi.
- pierwiastek kwadratowy y=√x, obliczone tylko dla x ≧ 0.
Oznaczając i=√(-1), wprowadzamy takie pojęcie jak liczba urojona, to usunie wszelkie ograniczenia z dziedziny definicji powyższych funkcji. Wyrażenia takie jak y=arcsin(2), y=ln(-4), y=√(-5) mają sens w pewnej przestrzeni liczb zespolonych.
Forma algebraiczna może być zapisana jako wyrażenie z=x + i×y na zbiorze rzeczywistych wartości xiy oraz i2 =-1.
Nowa koncepcja usuwa wszelkie ograniczenia dotyczące używania dowolnej funkcji algebraicznej i przypomina wykres linii prostej we współrzędnych wartości rzeczywistych i urojonych.
Złożony samolot
Geometryczna forma liczb zespolonych pozwala nam wizualnie przedstawić wiele ich właściwości. Na osi Re(z) zaznaczamy rzeczywiste wartości x, na Im(z) wartości urojone y, następnie punkt z na płaszczyźnie wyświetli wymaganą wartość zespoloną.
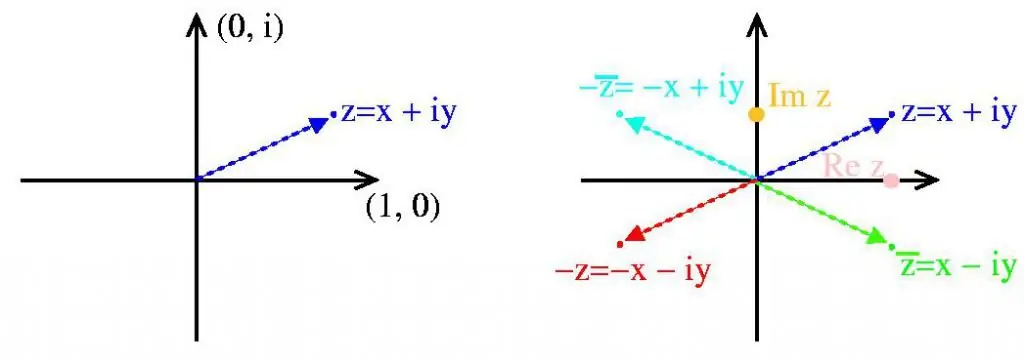
Definicje:
- Re(z) - oś rzeczywista.
- Im(z) - oznacza oś urojoną.
- z - punkt warunkowy liczby zespolonej.
- Nazywa się wartością liczbową długości wektora od zera do zmoduł.
- Osie rzeczywiste i urojone dzielą płaszczyznę na ćwiartki. Z dodatnią wartością współrzędnych - I kwartał. Gdy argument osi rzeczywistej jest mniejszy niż 0, a oś urojona jest większa niż 0 - II kwartał. Gdy współrzędne są ujemne - III kwartał. Ostatni, czwarty kwartał zawiera wiele dodatnich wartości rzeczywistych i ujemnych wartości urojonych.
Tak więc na płaszczyźnie z wartościami współrzędnych x i y zawsze można wizualizować punkt o liczbie zespolonej. Postać i jest wprowadzana, aby oddzielić część rzeczywistą od urojonej.
Właściwości
- Gdy wartość urojonego argumentu wynosi zero, otrzymujemy tylko liczbę (z=x), która znajduje się na rzeczywistej osi i należy do rzeczywistego zbioru.
- Szczególny przypadek, gdy wartość rzeczywistego argumentu wynosi zero, wyrażenie z=i×y odpowiada położeniu punktu na urojonej osi.
- Ogólna postać z=x + i×y będzie dla niezerowych wartości argumentów. Wskazuje położenie punktu charakteryzującego liczbę zespoloną w jednej z ćwiartek.
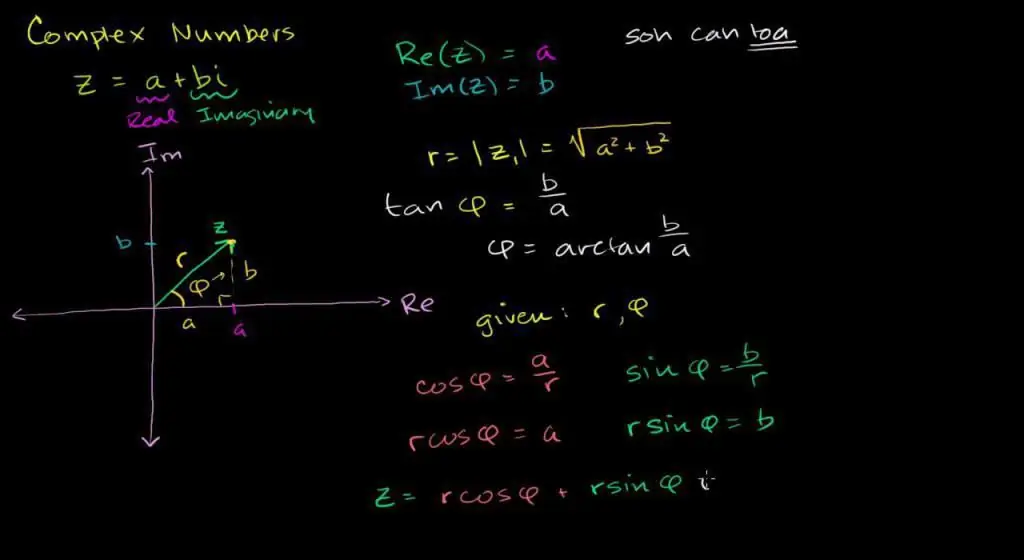
Zapis trygonometryczny
Przypomnij sobie biegunowy układ współrzędnych i definicję funkcji trygonometrycznych sin i cos. Jest oczywiste, że za pomocą tych funkcji można opisać położenie dowolnego punktu na płaszczyźnie. W tym celu wystarczy znać długość wiązki biegunowej oraz kąt nachylenia do osi rzeczywistej.
Definicja. Wpis postaci ∣z ∣ pomnożony przez sumę funkcji trygonometrycznych cos(ϴ) oraz części urojonej i ×sin(ϴ) nazywamy trygonometryczną liczbą zespoloną. Tutaj oznaczenie to kąt nachylenia do osi rzeczywistej
ϴ=arg(z) i r=∣z∣, długość belki.
Z definicji i właściwości funkcji trygonometrycznych wynika bardzo ważny wzór Moivre'a:
zn =r × (cos(n × ϴ) + i × sin(n × ϴ)).
Używając tego wzoru, wygodnie jest rozwiązywać wiele układów równań zawierających funkcje trygonometryczne. Zwłaszcza, gdy pojawia się problem wzniesienia się do władzy.
Moduł i faza
Aby uzupełnić opis złożonego zestawu, proponujemy dwie ważne definicje.
Znając twierdzenie Pitagorasa, łatwo obliczyć długość belki w biegunowym układzie współrzędnych.
r=∣z∣=√(x2 + y2), taki zapis na przestrzeni zespolonej nazywa się module” i charakteryzuje odległość od 0 do punktu na płaszczyźnie.
Kąt nachylenia złożonej belki do linii rzeczywistej ϴ jest powszechnie nazywany fazą.
Definicja pokazuje, że części rzeczywiste i urojone są opisane za pomocą funkcji cyklicznych. Mianowicie:
- x=r × cos(ϴ);
- y=r × grzech(ϴ);
Odwrotnie, faza jest powiązana z wartościami algebraicznymi poprzez wzór:
ϴ=arctan(x / y) + µ, wprowadzana jest poprawka µ, aby uwzględnić okresowość funkcji geometrycznych.
Formuła Eulera
Matematyczni często używają formy wykładniczej. Złożone liczby płaszczyzn są zapisywane jako wyrażenia
z=r × ei×ϴ , co wynika ze wzoru Eulera.

Ten rekord jest szeroko stosowany do praktycznego obliczania wielkości fizycznych. Forma prezentacji w formieWykładnicze liczby zespolone są szczególnie przydatne w obliczeniach inżynierskich, gdzie konieczne staje się obliczanie obwodów z prądami sinusoidalnymi oraz znajomość wartości całek funkcji z zadanym okresem. Same obliczenia służą jako narzędzie przy projektowaniu różnych maszyn i mechanizmów.
Określ operacje
Jak już wspomniano, wszystkie prawa algebraiczne dotyczące pracy z podstawowymi funkcjami matematycznymi mają zastosowanie do liczb zespolonych.
Operacja sumowania
Podczas dodawania wartości złożonych, dodawane są również ich części rzeczywiste i urojone.
z=z1 + z2 gdzie z1 i z2 - ogólne liczby zespolone. Przekształcając wyrażenie, po otwarciu nawiasów i uproszczeniu notacji otrzymujemy argument rzeczywisty x=(x1 + x2), argument urojony y=(y 1 + y2).
Na wykresie wygląda to jak dodanie dwóch wektorów, zgodnie z dobrze znaną regułą równoległoboku.
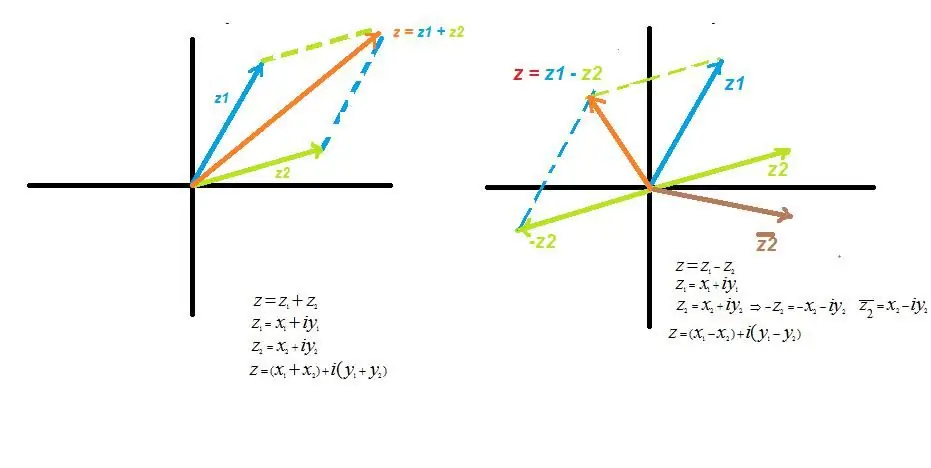
Operacja odejmowania
Rozważany jako szczególny przypadek dodawania, gdy jedna liczba jest dodatnia, a druga ujemna, to znaczy znajduje się w ćwiartce zwierciadła. Notacja algebraiczna wygląda jak różnica między częściami rzeczywistymi i urojonymi.
z=z1 - z2 lub biorąc pod uwagę wartości argumentów podobnie jak dodawanie operacji, otrzymujemy dla wartości rzeczywistych x=(x1 - x2) i urojonych y=(y1- y2).
Mnożenie na płaszczyźnie zespolonej
Korzystając z reguł pracy z wielomianami, wyprowadzamy wzórrozwiązywać liczby zespolone.
Postępując zgodnie z ogólnymi regułami algebraicznymi z=z1×z2, opisz każdy argument i wymień podobne. Części rzeczywiste i urojone można zapisać w następujący sposób:
- x=x1 × x2 - y1 × y2,
- y=x1 × y2 + x2 × y 1.
Piękniej wygląda, jeśli użyjemy wykładniczych liczb zespolonych.
Wyrażenie wygląda tak: z=z1 × z2 =r1 × eiϴ1 × r2 × eiϴ2=r1 × r2 × ei(ϴ1+ϴ2).
Co więcej, moduły są mnożone, a fazy są dodawane.
Oddział
Rozważając operację dzielenia jako odwrotność mnożenia, otrzymujemy proste wyrażenie w notacji wykładniczej. Dzielenie wartości z1 przez z2 jest wynikiem dzielenia ich modułów i różnicy faz. Formalnie, używając wykładniczej postaci liczb zespolonych, wygląda to tak:
z=z1 / z2 =r1 × e iϴ1 / r2 × ei ϴ2=r1 / r2× ei(ϴ1-ϴ 2).
W postaci notacji algebraicznej, operacja dzielenia liczb na płaszczyźnie zespolonej jest nieco bardziej skomplikowana:
z=z1 / z2.
Opisywanie argumentów i wykonywanie przekształceń wielomianowych ułatwia uzyskanie wartościx=x1 × x2 + y1 × y2, odpowiednio y=x2 × y1 - x1 × y2 jednak w obrębie opisywanej przestrzeni wyrażenie to ma sens, jeśli z2 ≠ 0.
Wyodrębnij korzeń
Wszystkie powyższe można zastosować podczas definiowania bardziej złożonych funkcji algebraicznych - podnoszenie do dowolnej potęgi i odwracanie jej - wydobywanie pierwiastka.
Używając ogólnej koncepcji podniesienia do potęgi n, otrzymujemy definicję:
zn =(r × eiϴ).
Używając wspólnych właściwości, przepisz jako:
zn =rn × eiϴ.
Otrzymaliśmy prosty wzór na podniesienie liczby zespolonej do potęgi.
Z definicji stopnia otrzymujemy bardzo ważną konsekwencję. Parzysta moc wyobrażonej jednostki wynosi zawsze 1. Każda nieparzysta moc wyobrażonej jednostki wynosi zawsze -1.
Teraz przestudiujmy funkcję odwrotną - wyodrębnianie pierwiastka.
Dla ułatwienia zapisu, weźmy n=2. Pierwiastek kwadratowy w z wartości zespolonej z na płaszczyźnie zespolonej C jest uważany za wyrażenie z=±, ważne dla każdego argumentu rzeczywistego większego lub równego zero. Dla w 0 nie ma rozwiązania.
Spójrzmy na najprostsze równanie kwadratowe z2 =1. Używając wzorów na liczby zespolone, przepisz r2 × ei2ϴ =r2 × ei2ϴ=ei0. Z zapisu widać, że r2 =1 i ϴ=0, zatem mamy jednoznaczne rozwiązanie równe 1. Ale to jest sprzeczne z poglądem, że z=-1 również pasuje do definicji pierwiastka kwadratowego.
Zastanówmy się, czego nie bierzemy pod uwagę. Jeśli przypomnimy sobie notację trygonometryczną, to przywracamy stwierdzenie - przy okresowej zmianie fazy ϴ liczba zespolona się nie zmienia. Niech p oznacza wartość okresu, wtedy mamy r2 × ei2ϴ =ei(0+p), gdzie 2ϴ=0 + p lub ϴ=p / 2. Dlatego ei0 =1 i eip/2 =-1. Otrzymaliśmy drugie rozwiązanie, które odpowiada ogólnemu rozumieniu pierwiastka kwadratowego.
Więc, aby znaleźć dowolny pierwiastek liczby zespolonej, zastosujemy procedurę.
- Zapisz formę wykładniczą w=∣w∣ × ei(arg (w) + pk), k jest dowolną liczbą całkowitą.
- Pożądana liczba jest również reprezentowana w formie Eulera z=r × eiϴ.
- Użyj ogólnej definicji funkcji wyodrębniania korzeni r ei ϴ =∣w∣ × ei(arg(w) + pk).
- Z ogólnych własności równości modułów i argumentów piszemy rn =∣w∣ i nϴ=arg (w) + p×k.
- Ostateczny rekord pierwiastka liczby zespolonej jest opisany wzorem z=√∣w∣ × ei ( arg (w) + pk ) / .
- Uwaga. Wartość ∣w∣, z definicji,jest dodatnią liczbą rzeczywistą, więc pierwiastek dowolnego stopnia ma sens.
Pole i koniugacja
Na zakończenie podajemy dwie ważne definicje, które mają niewielkie znaczenie dla rozwiązywania problemów stosowanych z liczbami zespolonymi, ale są niezbędne dla dalszego rozwoju teorii matematycznej.
Wyrażenia dodawania i mnożenia tworzą pole, jeśli spełniają aksjomaty dla dowolnych elementów płaszczyzny zespolonej z:
- Złożona suma nie zmienia się wraz ze zmianą miejsc złożonych terminów.
- Oświadczenie jest prawdziwe - w wyrażeniu złożonym dowolna suma dwóch liczb może zostać zastąpiona ich wartością.
- Istnieje neutralna wartość 0, dla której z + 0=0 + z=z jest prawdą.
- Dla każdego z istnieje przeciwieństwo - z, do którego dodawanie daje zero.
- Podczas zmiany miejsc złożonych czynników, złożony produkt się nie zmienia.
- Mnożenie dowolnych dwóch liczb można zastąpić ich wartością.
- Istnieje neutralna wartość 1, przez którą mnożenie nie zmienia liczby zespolonej.
- Dla każdego z ≠ 0 występuje odwrotność z-1, która mnoży się przez 1.
- Pomnożenie sumy dwóch liczb przez trzecią jest równoznaczne z pomnożeniem każdej z nich przez tę liczbę i dodaniem wyników.
- 0 ≠ 1.
Liczby z1 =x + i×y oraz z2 =x - i×y nazywane są sprzężonymi.
Twierdzenie. W przypadku koniugacji zdanie jest prawdziwe:
- Koniugacja sumy jest równa sumie sprzężonych elementów.
- Koniugat produktu toprodukt koniugacji.
- Koniugacja koniugacji jest równa samej liczbie.
W ogólnej algebrze takie własności są nazywane automorfizmami pól.
Przykłady
Postępując zgodnie z podanymi regułami i wzorami liczb zespolonych, możesz z nimi łatwo operować.
Rozważmy najprostsze przykłady.
Problem 1. Korzystając z równania 3y +5 x i=15 - 7i, wyznacz x i y.
Decyzja. Przypomnij sobie definicję równości zespolonych, wtedy 3y=15, 5x=-7. Dlatego x=-7 / 5, y=5.
Zadanie 2. Oblicz wartości 2 + i28 i 1 + i135.
Decyzja. Oczywiście 28 jest liczbą parzystą, wynikającą z definicji liczby zespolonej w potędze i28 =1, co oznacza, że wyrażenie 2 + i 28 =3. Druga wartość, i135 =-1, potem 1 + i135 =0.
Zadanie 3. Oblicz iloczyn wartości 2 + 5i i 4 + 3i.
Decyzja. Z ogólnych własności mnożenia liczb zespolonych otrzymujemy (2 + 5i)X(4 + 3i)=8 - 15 + i(6 + 20). Nowa wartość to -7 + 26i.
Zadanie 4. Oblicz pierwiastki z równania z3 =-i.
Decyzja. Istnieje kilka sposobów na znalezienie liczby zespolonej. Rozważmy jedno z możliwych. Z definicji ∣ - i∣=1, fazą dla -i jest -p / 4. Oryginalne równanie można przepisać jako r3ei3ϴ =e-p/4+pk, skąd z=e-p / 12 + pk/3, dla dowolnej liczby całkowitej k.
Zestaw rozwiązań ma postać (e-ip/12,eip/4, ei2 p/3).
Dlaczego potrzebujemy liczb zespolonych
Historia zna wiele przykładów, kiedy naukowcy pracujący nad teorią nawet nie myślą o praktycznym zastosowaniu ich wyników. Matematyka to przede wszystkim gra umysłu, ścisłe trzymanie się związków przyczynowo-skutkowych. Prawie wszystkie konstrukcje matematyczne sprowadzają się do rozwiązywania równań całkowych i różniczkowych, a te z kolei, z pewnym przybliżeniem, rozwiązuje się, znajdując pierwiastki wielomianów. Tutaj po raz pierwszy spotykamy się z paradoksem liczb urojonych.
Naukowcy przyrodnicy, rozwiązując całkowicie praktyczne problemy, odwołując się do rozwiązań różnych równań, odkrywają matematyczne paradoksy. Interpretacja tych paradoksów prowadzi do absolutnie zdumiewających odkryć. Jednym z takich przykładów jest podwójna natura fal elektromagnetycznych. Liczby zespolone odgrywają kluczową rolę w zrozumieniu ich własności.
To z kolei znalazło praktyczne zastosowanie w optyce, elektronice radiowej, energetyce i wielu innych dziedzinach technologicznych. Kolejny przykład, znacznie trudniejszy do zrozumienia zjawisk fizycznych. Antymateria była przewidziana na końcu długopisu. I dopiero wiele lat później rozpoczynają się próby jego fizycznej syntezy.
Nie myśl, że tylko w fizyce są takie sytuacje. Nie mniej interesujących odkryć dokonuje się w dzikiej przyrodzie, w syntezie makrocząsteczek, podczas badań nad sztuczną inteligencją. A to wszystko dziękiposzerzanie naszej świadomości, odchodzenie od prostego dodawania i odejmowania wartości przyrodniczych.






