Gazy, z punktu widzenia termodynamiki, są opisane przez zestaw cech makroskopowych, z których główne to temperatura, ciśnienie i objętość. Stałość jednego z tych parametrów i zmiana dwóch pozostałych wskazuje, że w gazie zachodzi taki lub inny izoproces. Poświęcimy ten artykuł szczegółowej odpowiedzi na pytania, że jest to proces izochoryczny, czym różni się od izotermicznych i izobarycznych zmian stanów układu gazowego.
Gaz idealny w fizyce

Zanim odpowiesz na pytanie, że jest to proces izochoryczny, powinieneś lepiej poznać pojęcie gazu doskonałego. W fizyce jest rozumiany jako każdy gaz, w którym średnia energia kinetyczna cząstek składowych znacznie przekracza energię potencjalną ich interakcji, a odległości między tymi cząstkami są o kilka rzędów wielkości większe niż ich wymiary liniowe. W podanych warunkach jest to możliwe, podczas wykonywaniaobliczenia nie uwzględniają energii oddziaływania między cząstkami (jest równa zeru), a ponadto można założyć, że cząstki są punktami materialnymi o określonej masie m.
Jedynym procesem zachodzącym w gazie doskonałym jest zderzenie cząstek ze ściankami naczynia zawierającego substancję. Zderzenia te w praktyce objawiają się istnieniem pewnego ciśnienia w gazie P.
Z reguły każdą substancję gazową, która składa się ze stosunkowo obojętnych chemicznie cząsteczek i która ma niskie ciśnienie i wysokie temperatury, może być uważana za gaz doskonały z wystarczającą dokładnością do praktycznych obliczeń.
Równanie opisujące gaz doskonały
Oczywiście mówimy o uniwersalnym prawie Clapeyrona-Mendeleeva, które należy dobrze zrozumieć, aby zrozumieć, że jest to proces izochoryczny. Zatem uniwersalne równanie stanu ma następującą postać:
PV=nRT.
Oznacza to, że iloczyn ciśnienia P i objętości gazu V jest równy iloczynowi temperatury bezwzględnej T i ilości substancji w molach n, gdzie R jest współczynnikiem proporcjonalności. Samo równanie po raz pierwszy spisał Emile Clapeyron w 1834 r., A w latach 70. XIX wieku D. Mendelejew zastąpił w nim zestaw stałych wartości pojedynczej uniwersalnej stałej gazowej R (8,314 J/(molK)).
Zgodnie z równaniem Clapeyrona-Mendeleeva, w układzie zamkniętym liczba cząstek gazu pozostaje stała, więc tylko trzy parametry makroskopowe mogą się zmieniać (T, Pi V). Ten ostatni fakt leży u podstaw zrozumienia różnych izoprocesów, które zostaną omówione poniżej.
Co to jest proces izochoryczny?
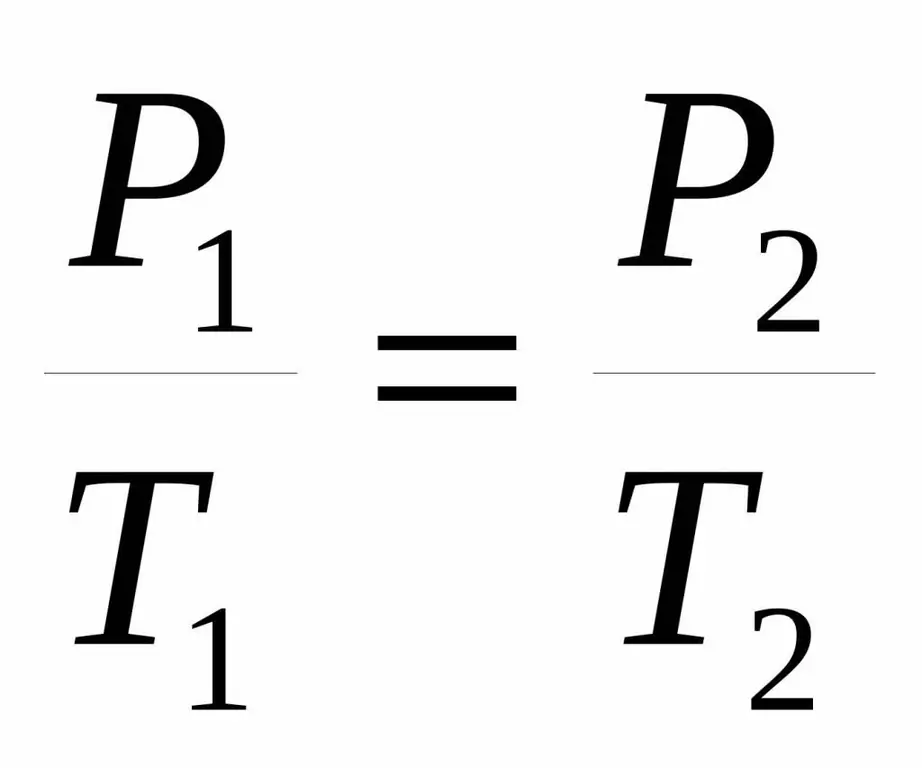
Ten proces jest rozumiany jako absolutnie każda zmiana stanu systemu, w którym zachowana jest jego objętość.
Jeśli przejdziemy do uniwersalnego równania stanu, możemy powiedzieć, że w procesie izochorycznym w gazie zmienia się tylko ciśnienie i temperatura bezwzględna. Aby dokładnie zrozumieć, jak zmieniają się parametry termodynamiczne, piszemy odpowiednie wyrażenie matematyczne:
P / T=const.
Czasami ta równość jest podana w nieco innej formie:
P1 / T1=P2 / T 2.
Oba równouprawnienia nazywane są prawem Karola, od nazwiska francuskiego naukowca, który pod koniec XVIII wieku eksperymentalnie uzyskał odnotowaną zależność.

Jeśli zbudujemy wykres funkcji P(T), to otrzymamy zależność liniową, którą nazywamy izochorem. Każdy izochor (dla wszystkich wartości n i V) jest linią prostą.
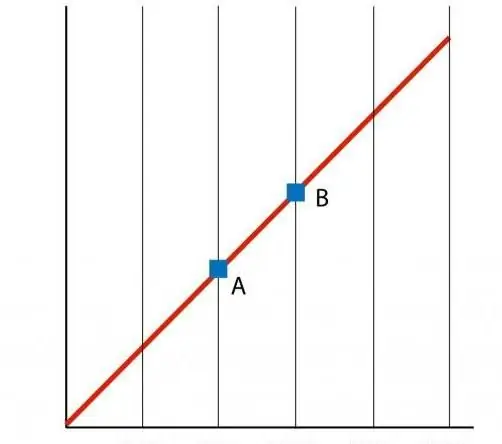
Opis energetyczny procesu
Jak wspomniano, proces izochoryczny to zmiana stanu systemu, która zachodzi w systemie zamkniętym, ale nie izolowanym. Mówimy o możliwości wymiany ciepła między gazem a otoczeniem. Ogólnie rzecz biorąc, każde dostarczenie ciepła Q do systemu prowadzi do dwóch wyników:
- zmienia energię wewnętrzną U;
- gazczy działa A, rozszerzając się lub kurcząc.
Ostatnie wnioskowanie jest zapisane matematycznie w następujący sposób:
Q=U + A.
Proces izochoryczny gazu doskonałego, z definicji, nie oznacza pracy wykonanej przez gaz, ponieważ jego objętość pozostaje niezmieniona. Oznacza to, że całe ciepło dostarczane do systemu idzie na zwiększenie jego energii wewnętrznej:
Q=U.
Jeżeli do tego wyrażenia podstawimy wyraźny wzór na energię wewnętrzną, to ciepło procesu izochorycznego można przedstawić jako:
Q=z / 2nRT.
Tutaj z jest liczbą stopni swobody, która jest określona przez wieloatomową naturę cząsteczek tworzących gaz. Dla gazu jednoatomowego z=3, dla gazu dwuatomowego - 5, a dla gazu trójatomowego i więcej - 6. Tutaj pod stopniami swobody mamy na myśli stopnie translacyjne i rotacyjne.
Jeżeli porównamy sprawność ogrzewania instalacji gazowej w procesach izochorycznych i izobarycznych, to w pierwszym przypadku uzyskamy maksymalną sprawność, ponieważ podczas izobarycznej zmiany stanu układu gaz rozpręża się i część dopływu ciepła przeznaczana jest na wykonywanie pracy.
Proces izobaryczny
Powyżej szczegółowo opisaliśmy, że jest to proces izochoryczny. Teraz powiedzmy kilka słów o innych izoprocesach. Zacznijmy od izobaryki. Na podstawie nazwy jest rozumiany jako przejście systemu między stanami przy stałym ciśnieniu. Proces ten jest opisany przez prawo Gay-Lussaca w następujący sposób:
V / T=const.
Podobnie jak w przypadku izochory, izobar V(T) również reprezentuje linię prostą na wykresie.
Zadowolnego procesu izobarycznego wygodnie jest obliczyć pracę wykonaną przez gaz, ponieważ jest ona równa iloczynowi stałego ciśnienia i zmiany objętości.
Proces izotermiczny
Jest to proces, w którym temperatura systemu pozostaje stała. Jest on opisany przez prawo Boyle'a-Mariotte'a dla gazu doskonałego. Warto zauważyć, że jest to pierwsze odkryte eksperymentalnie prawo gazowe (druga połowa XVII wieku). Jego zapis matematyczny wygląda tak:
PV=const.
Procesy izochoryczne i izotermiczne różnią się pod względem reprezentacji graficznej, ponieważ funkcja P(V) jest zależnością hiperboliczną, a nie liniową.
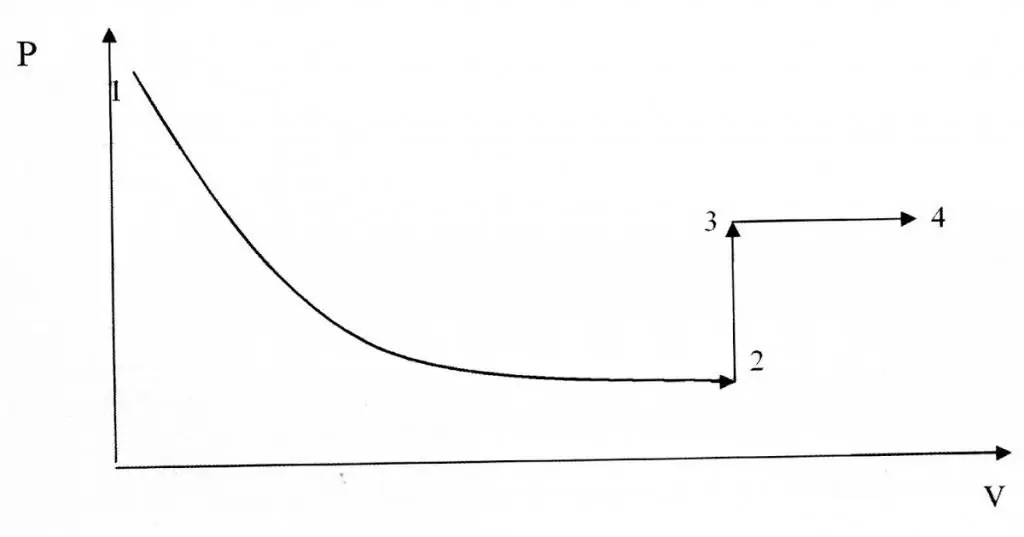
Przykład rozwiązywania problemów
Skonsolidujmy informacje teoretyczne zawarte w artykule poprzez ich zastosowanie do rozwiązania praktycznego problemu. Wiadomo, że czysty azot gazowy znajdował się w butli pod ciśnieniem 1 atmosfery i w temperaturze 25°C. Po podgrzaniu butli gazowej i zmierzeniu w niej ciśnienia okazało się, że wynosi 1,5 atmosfery. Jaka jest temperatura gazu w butli po podgrzaniu? O ile zmieniła się energia wewnętrzna gazu, jeśli w balonie były 4 mole azotu.
Aby odpowiedzieć na pierwsze pytanie, używamy następującego wyrażenia:
P1 / T1=P2 / T 2.
Skąd się bierzemy:
T2=P2 / P1 T 1.
W tym wyrażeniu ciśnienie można zastąpić dowolnymi jednostkamipomiarów, ponieważ kurczą się, a temperatura jest tylko w stopniach Kelvina. Powiedziawszy to, otrzymujemy:
T2=1,5 /1298,15=447,224 K.
Wyliczona temperatura w stopniach Celsjusza wynosi 174 °C.
Ponieważ cząsteczka azotu jest dwuatomowa, zmianę jej energii wewnętrznej podczas ogrzewania można określić w następujący sposób:
ΔU=5 / 2nRΔT.
Podstawiając znane wartości do tego wyrażenia, otrzymamy odpowiedź na drugie pytanie problemu: ΔU=+12.4 kJ.






