W termodynamice, badając przejścia od stanu początkowego do końcowego systemu, ważne jest poznanie efektu cieplnego procesu. Pojęcie pojemności cieplnej jest ściśle związane z tym efektem. W tym artykule rozważymy pytanie, co należy rozumieć przez izochoryczną pojemność cieplną gazu.
Gaz idealny
Gaz doskonały to gaz, którego cząsteczki są uważane za punkty materialne, to znaczy nie mają wymiarów, ale masę, i w którym cała energia wewnętrzna składa się wyłącznie z energii kinetycznej ruchu cząsteczek i atomy.
Żaden prawdziwy gaz idealnie nigdy nie spełni opisanego modelu, ponieważ jego cząstki wciąż mają pewne wymiary liniowe i oddziałują ze sobą za pomocą słabych wiązań van der Waalsa lub wiązań chemicznych innego typu. Jednak przy niskich ciśnieniach i wysokich temperaturach odległości między cząsteczkami są duże, a ich energia kinetyczna kilkadziesiąt razy przewyższa energię potencjalną. Wszystko to umożliwia zastosowanie z dużą dokładnością idealnego modelu dla gazów rzeczywistych.
Wewnętrzna energia gazu
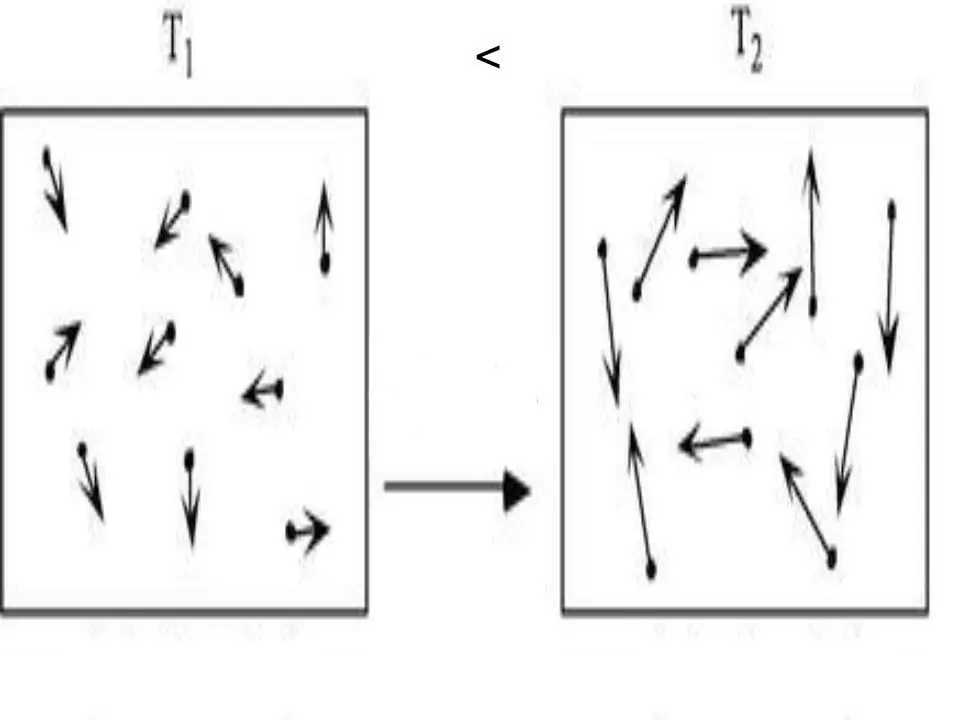
Wewnętrzna energia dowolnego układu jest cechą fizyczną, która jest równa sumie energii potencjalnej i kinetycznej. Ponieważ energia potencjalna może być pominięta w gazach doskonałych, możemy zapisać dla nich równość:
U=Ek.
Gdzie Ek to energia układu kinetycznego. Korzystając z teorii kinetyki molekularnej i stosując uniwersalne równanie stanu Clapeyrona-Mendeleeva, nie jest trudno uzyskać wyrażenie na U. Jest ono napisane poniżej:
U=z/2nRT.
Tutaj T, R i n to odpowiednio temperatura bezwzględna, stała gazowa i ilość substancji. Wartość z jest liczbą całkowitą wskazującą liczbę stopni swobody, jaką ma cząsteczka gazu.
Izobaryczna i izochoryczna pojemność cieplna
W fizyce pojemność cieplna to ilość ciepła, która musi zostać dostarczona do badanego systemu, aby ogrzał go o jeden kelwin. Odwrotna definicja jest również prawdziwa, to znaczy pojemność cieplna to ilość ciepła, które system uwalnia po schłodzeniu o jeden kelwin.
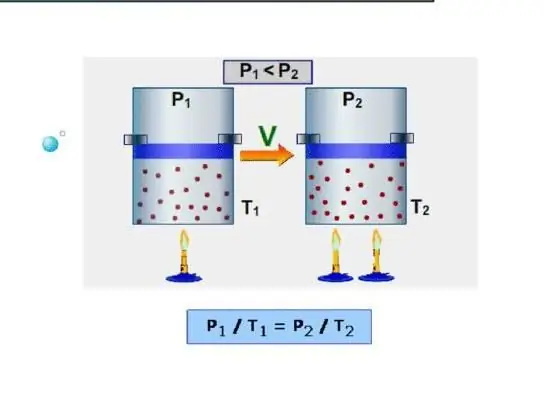
Najłatwiejszym sposobem dla systemu jest określenie izochorycznej pojemności cieplnej. Jest rozumiany jako pojemność cieplna przy stałej objętości. Ponieważ system nie wykonuje pracy w takich warunkach, cała energia jest wydatkowana na zwiększenie wewnętrznych rezerw energii. Oznaczmy izochoryczną pojemność cieplną symbolem CV, wtedy możemy napisać:
dU=CVdT.
To jest zmiana energii wewnętrznejsystem jest wprost proporcjonalny do zmiany jego temperatury. Jeśli porównamy to wyrażenie z równością zapisaną w poprzednim akapicie, otrzymamy wzór na CV w gazie doskonałym:
СV=z/2nR.
Ta wartość jest niewygodna w praktyce, ponieważ zależy od ilości substancji w systemie. W związku z tym wprowadzono pojęcie izochorycznej pojemności cieplnej właściwej, czyli wartości obliczanej na 1 mol gazu lub na 1 kg. Pierwszą wartość oznaczmy symbolem CV, drugą - symbolem CV m. Dla nich możesz napisać następujące formuły:
CV=z/2R;
CVm=z/2R/M.
Tu M to masa molowa.
Izobaryczny to pojemność cieplna przy utrzymaniu stałego ciśnienia w systemie. Przykładem takiego procesu jest rozprężanie się gazu w cylindrze pod tłokiem podczas jego podgrzewania. W przeciwieństwie do procesu izochorycznego, podczas procesu izobarycznego ciepło dostarczane do układu jest zużywane na zwiększenie energii wewnętrznej i wykonanie pracy mechanicznej, czyli:
H=dU + PdV.
Entalpia procesu izobarycznego jest iloczynem izobarycznej pojemności cieplnej i zmiany temperatury w układzie, czyli:
H=CPdT.
Jeśli weźmiemy pod uwagę rozszerzanie przy stałym ciśnieniu 1 mola gazu, to pierwsza zasada termodynamiki będzie zapisana jako:
CPdT=CV dT + RdT.
Ostatni wyraz otrzymujemy z równaniaClapeyron-Mendeleev. Z tej równości wynika zależność między pojemnościami cieplnymi izobarycznymi i izochorycznymi:
CP=CV + R.
Dla gazu doskonałego, molowa pojemność cieplna przy stałym ciśnieniu jest zawsze większa niż odpowiadająca jej charakterystyka izochoryczna przy R=8, 314 J/(molK).
Stopień swobody cząsteczek i pojemność cieplna
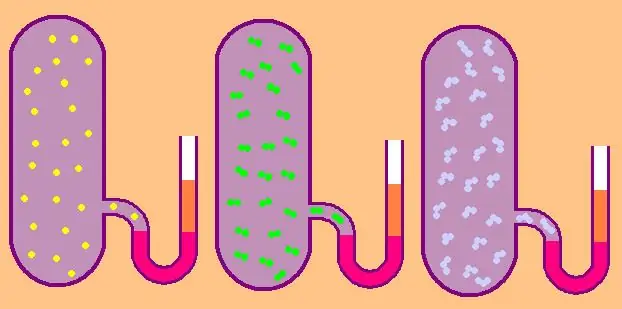
Napiszmy ponownie wzór na konkretną molową pojemność cieplną izochoryczną:
CV=z/2R.
W przypadku gazu jednoatomowego wartość z=3, ponieważ atomy w przestrzeni mogą poruszać się tylko w trzech niezależnych kierunkach.
Jeśli mówimy o gazie składającym się z cząsteczek dwuatomowych, na przykład tlenu O2 lub wodoru H2, to oprócz ruchu translacyjnego, cząsteczki te mogą nadal obracać się wokół dwóch wzajemnie prostopadłych osi, to znaczy z będzie równe 5.
Dla bardziej złożonych cząsteczek użyj z=6. do określenia CV






