Przyspieszenie i prędkość to dwie ważne cechy kinematyczne każdego rodzaju ruchu. Znajomość zależności tych wielkości od czasu pozwala obliczyć drogę pokonywaną przez organizm. Ten artykuł zawiera odpowiedź na pytanie, jak znaleźć przyspieszenie, znając prędkość i czas.
Pojęcie prędkości i przyspieszenia
Zanim udzielimy odpowiedzi na pytanie, jak, znając prędkość i czas, znaleźć przyspieszenie, rozważmy każdą z cech z punktu widzenia fizyki.
Prędkość to wartość określająca prędkość zmiany współrzędnych w przestrzeni podczas ruchu ciała. Prędkość obliczana jest według wzoru:
v=dl/dt.
Gdzie dl jest ścieżką przebytą przez ciało w czasie dt. Prędkość jest zawsze skierowana wzdłuż stycznej na ścieżce ruchu.
Ruch może odbywać się ze stałą prędkością w czasie lub ze zmienną prędkością. W tym drugim przypadku mówimy o obecności przyspieszenia. W fizyce przyspieszenie określa szybkość zmian v, która jest zapisana jako wzór:
a=dv/dt.
Ta równość jest odpowiedzią na pytanie, jak znaleźćprzyspieszenie prędkości. Aby to zrobić, wystarczy wykonać pierwszą pochodną czasową v.
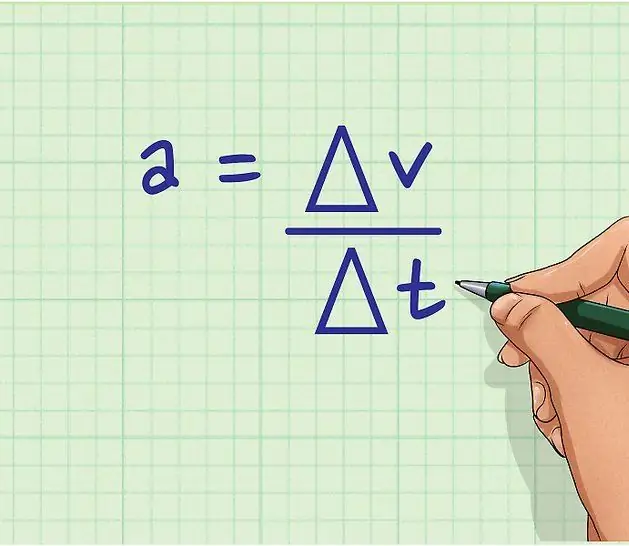
Kierunek przyspieszenia pokrywa się z kierunkiem różnicy wektorów prędkości. W przypadku ruchu prostoliniowego przyspieszonego wielkości a i v są skierowane w tym samym kierunku.
Jak znaleźć przyspieszenie przy danej prędkości i czasie?
Podczas studiowania mechaniki najpierw bierze się pod uwagę jednorodne i jednostajnie przyspieszone rodzaje ruchu po prostej trajektorii. W obu przypadkach do określenia przyspieszenia należy wybrać przedział czasu Δt. Następnie należy określić wartości prędkości v1 i v2 na końcach tego przedziału. Średnie przyspieszenie definiuje się w następujący sposób:
a=(v2- v1)/Δt.
W przypadku ruchu jednostajnego prędkość pozostaje stała (v2=v1), więc wartość woli być zero. W przypadku ruchu jednostajnie przyspieszonego wartość a będzie stała, a więc nie zależy od przedziału czasu Δt we wzorze.
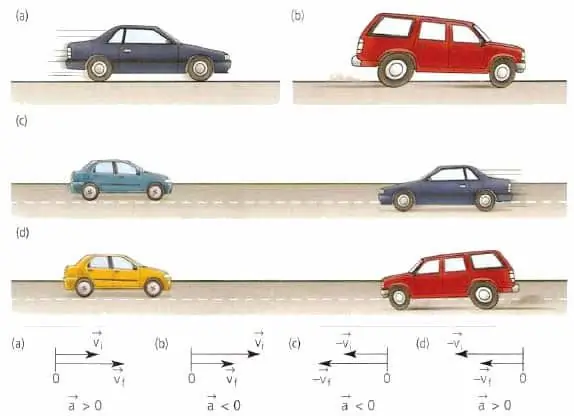
W przypadku bardziej skomplikowanych przypadków ruchu, gdy prędkość jest funkcją czasu, należy skorzystać ze wzoru na pochodną przez a, który został przedstawiony w powyższym akapicie.
Przykład rozwiązywania problemów
Po ustaleniu, jak znaleźć przyspieszenie, znając czas i prędkość, rozwiążemy prosty problem. Załóżmy, że ciało poruszające się po określonej trajektorii zmienia swoją prędkość zgodnie z następującym równaniem:
v=3t2- t + 4.
Jakie będzie przyspieszenie ciała w czasie t=5 sekund?
Przyspieszenie jest pierwszą pochodną v względem zmiennej t, mamy:
a=dv/dt=6t - 1.
Aby odpowiedzieć na pytanie dotyczące problemu, należy podstawić znaną wartość czasu do otrzymanego równania: a=29 m/c2.






