Ważnym działem termodynamiki jest badanie przemian między różnymi fazami substancji, ponieważ procesy te zachodzą w praktyce i mają fundamentalne znaczenie dla przewidywania zachowania układu w określonych warunkach. Te przemiany nazywane są przejściami fazowymi, którym poświęcony jest artykuł.
Koncepcja fazy i elementu systemu

Przed przystąpieniem do rozważań o przejściach fazowych w fizyce konieczne jest zdefiniowanie pojęcia samej fazy. Jak wiadomo z kursu fizyki ogólnej, istnieją trzy stany skupienia materii: gazowy, stały i ciekły. W specjalnej części nauki - w termodynamice - prawa formułowane są dla faz materii, a nie dla ich stanów skupienia. Przez fazę rozumie się pewną objętość materii, która ma jednorodną strukturę, charakteryzuje się określonymi właściwościami fizycznymi i chemicznymi oraz jest oddzielona od reszty materii granicami, które nazywamy interfazą.
Tak więc pojęcie „fazy” niesie ze sobą znacznie więcej praktycznie istotnych informacji o właściwościachbardziej niż stan skupienia. Na przykład stan stały metalu, takiego jak żelazo, może znajdować się w następujących fazach: niskotemperaturowy magnetyczny centrowany na ciele (BCC), niskotemperaturowy niemagnetyczny sześcienny (BCC), niskotemperaturowy niemagnetyczny sześcienny (fcc) i wysoko- temperatura niemagnetyczna bcc.
Oprócz pojęcia „fazy”, prawa termodynamiki używają również terminu „składniki”, co oznacza liczbę pierwiastków chemicznych, które składają się na dany układ. Oznacza to, że faza może być jednoskładnikowa (1 pierwiastek chemiczny) lub wieloskładnikowa (kilka pierwiastków chemicznych).
Twierdzenie Gibbsa i równowaga między fazami układu

Aby zrozumieć przejścia fazowe, konieczne jest poznanie warunków równowagi między nimi. Warunki te można matematycznie uzyskać, rozwiązując układ równań Gibbsa dla każdego z nich, zakładając, że stan równowagi zostaje osiągnięty, gdy całkowita energia Gibbsa układu odizolowanego od wpływu zewnętrznego przestaje się zmieniać.
W wyniku rozwiązania wskazanego układu równań uzyskuje się warunki do istnienia równowagi między kilkoma fazami: izolowany układ przestanie ewoluować tylko wtedy, gdy ciśnienia, potencjały chemiczne każdego składnika i temperatury we wszystkich fazach są sobie równe.
Reguła faz Gibbsa dla równowagi

Układ składający się z kilku faz i komponentów może być w równowadze nie tylkow określonych warunkach, na przykład w określonej temperaturze i ciśnieniu. Niektóre zmienne w twierdzeniu Gibbsa dla równowagi można zmienić, zachowując zarówno liczbę faz, jak i liczbę składników, które są w tej równowadze. Liczbę zmiennych, które można zmienić bez naruszania równowagi w układzie, nazywamy liczbą swobód tego układu.
Liczba swobód l systemu składającego się z faz f i składników k jest jednoznacznie określona z reguły faz Gibbsa. Ta reguła jest matematycznie zapisana w następujący sposób: l + f=k + 2. Jak pracować z tą regułą? Bardzo prosta. Na przykład wiadomo, że układ składa się z f=3 faz równowagi. Jaka jest minimalna liczba elementów, które może zawierać taki system? Możesz odpowiedzieć na pytanie, rozumując w następujący sposób: w przypadku równowagi najbardziej rygorystyczne warunki istnieją, gdy jest ona realizowana tylko przy określonych wskaźnikach, to znaczy zmiana dowolnego parametru termodynamicznego doprowadzi do braku równowagi. Oznacza to, że liczba swobód l=0. Zastępując znane wartości l i f, otrzymujemy k=1, czyli układ, w którym trzy fazy są w równowadze, może składać się z jednego składnika. Doskonałym przykładem jest punkt potrójny wody, w którym lód, woda w stanie ciekłym i para występują w równowadze w określonych temperaturach i ciśnieniach.
Klasyfikacja przemian fazowych
Jeśli zaczniesz zmieniać niektóre parametry termodynamiczne w układzie w równowadze, możesz zaobserwować, jak jedna faza zniknie, a pojawi się inna. Prostym przykładem tego procesu jest topienie lodu podczas podgrzewania.
Biorąc pod uwagę, że równanie Gibbsa zależy tylko od dwóch zmiennych (ciśnienia i temperatury), a przejście fazowe wiąże się ze zmianą tych zmiennych, to matematycznie przejście między fazami można opisać przez zróżnicowanie energii Gibbsa w odniesieniu do jej zmienne. Właśnie to podejście zostało zastosowane przez austriackiego fizyka Paula Ehrenfesta w 1933 roku, kiedy opracował klasyfikację wszystkich znanych procesów termodynamicznych, które zachodzą wraz ze zmianą równowagi fazowej.
Z podstaw termodynamiki wynika, że pierwsza pochodna energii Gibbsa względem temperatury jest równa zmianie entropii układu. Pochodna energii Gibbsa względem ciśnienia jest równa zmianie objętości. Jeśli, gdy zmieniają się fazy w systemie, entropia lub objętość ulegają przerwaniu, to znaczy zmieniają się nagle, to mówi się o przejściu fazowym pierwszego rzędu.
Ponadto, drugą pochodną energii Gibbsa w odniesieniu do temperatury i ciśnienia są odpowiednio pojemność cieplna i współczynnik rozszerzalności objętościowej. Jeśli transformacji między fazami towarzyszy nieciągłość wartości wskazanych wielkości fizycznych, to mówi się o przejściu fazowym drugiego rzędu.
Przykłady przekształceń między fazami

W naturze występuje ogromna liczba różnych przejść. W ramach tej klasyfikacji uderzającymi przykładami przejść pierwszego rodzaju są procesy topienia metali lub kondensacji pary wodnej z powietrza, gdy w układzie następuje skok objętości.
Jeśli mówimy o przejściach drugiego rzędu, uderzającymi przykładami są przemiany żelaza ze stanu magnetycznego w paramagnetyczny w temperaturze768 ºC lub przekształcenie metalowego przewodnika w stan nadprzewodzący w temperaturach bliskich zeru bezwzględnemu.
Równania opisujące przejścia pierwszego rodzaju
W praktyce często trzeba wiedzieć, jak zmienia się temperatura, ciśnienie i pochłonięta (uwolniona) energia w układzie, gdy zachodzą w nim przemiany fazowe. W tym celu wykorzystywane są dwa ważne równania. Uzyskuje się je w oparciu o znajomość podstaw termodynamiki:
- Wzór Clapeyrona, który określa zależność między ciśnieniem a temperaturą podczas przemian między różnymi fazami.
- Wzór Clausiusa, który łączy pochłoniętą (uwolnioną) energię i temperaturę układu podczas transformacji.
Zastosowanie obu równań służy nie tylko do uzyskania ilościowych zależności wielkości fizycznych, ale także do wyznaczenia znaku nachylenia krzywych równowagi na diagramach fazowych.
Równanie opisujące przejścia drugiego rodzaju

Przejścia fazowe pierwszego i drugiego rodzaju są opisane różnymi równaniami, ponieważ zastosowanie równań Clausiusa i Clausiusa do przejść drugiego rzędu prowadzi do matematycznej niepewności.
Do opisania tego ostatniego używa się równań Ehrenfesta, które ustalają związek między zmianami ciśnienia i temperatury dzięki znajomości zmian pojemności cieplnej i współczynnika rozszerzalności objętościowej podczas procesu transformacji. Równania Ehrenfesta służą do opisu przejść przewodnik-nadprzewodnik przy braku pola magnetycznego.
Ważnośćdiagramy fazowe
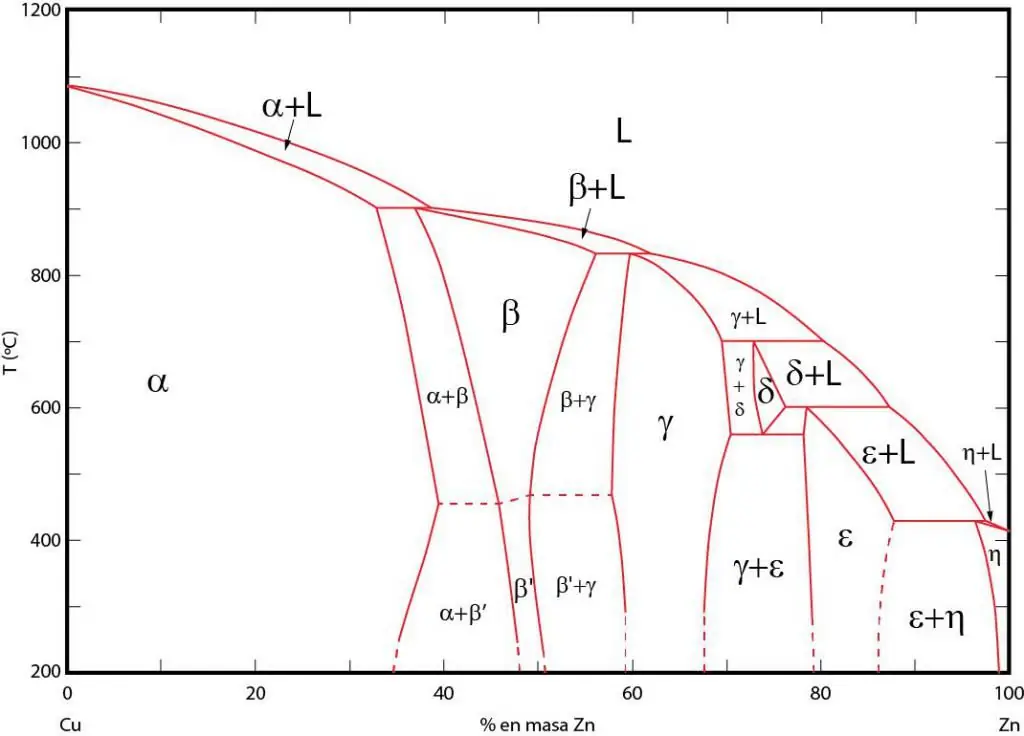
Diagramy fazowe to graficzna reprezentacja obszarów, w których odpowiednie fazy istnieją w równowadze. Obszary te są oddzielone liniami równowagi między fazami. Często stosuje się wykresy fazowe P-T (ciśnienie-temperatura), T-V (temperatura-objętość) i P-V (ciśnienie-objętość).
Ważność diagramów fazowych polega na tym, że pozwalają one przewidzieć, w jakiej fazie będzie system, gdy zmienią się odpowiednio warunki zewnętrzne. Informacje te są wykorzystywane w obróbce cieplnej różnych materiałów w celu uzyskania struktury o pożądanych właściwościach.






