Ze szkoły wszyscy znamy zasadę podnoszenia do potęgi: dowolna liczba z wykładnikiem N jest równa wynikowi pomnożenia tej liczby przez samą N razy. Innymi słowy, 7 do potęgi 3 to 7 pomnożone przez siebie trzy razy, czyli 343. Inną zasadą jest to, że podniesienie dowolnej wartości do potęgi 0 daje jeden, a podniesienie wartości ujemnej jest wynikiem zwykłego potęgowania, jeśli jest parzysty i ten sam wynik ze znakiem minus, jeśli jest nieparzysty.

Zasady dają również odpowiedź, jak podnieść liczbę do potęgi ujemnej. Aby to zrobić, musisz w zwykły sposób podnieść wymaganą wartość o moduł wskaźnika, a następnie podzielić jednostkę przez wynik.
Z tych zasad jasno wynika, że realizacja rzeczywistych zadań w dużych ilościach będzie wymagała dostępności środków technicznych. Ręcznie będzie można pomnożyć przez siebie maksymalny zakres liczb do dwudziestu lub trzydziestu, a potem nie więcej niż trzy lub cztery razy. Nie wspominając o tym, że wtedy również podzielmy jednostkę przez wynik. Dlatego dla tych, którzy nie mają pod ręką specjalnej inżynieriikalkulator, pokażemy Ci, jak podnieść liczbę do potęgi ujemnej w programie Excel.
Rozwiązywanie problemów w programie Excel
Aby rozwiązać problemy z potęgowaniem, Excel umożliwia użycie jednej z dwóch opcji.
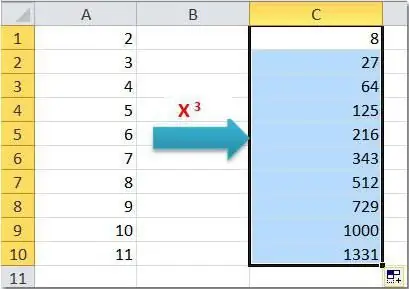
Pierwszym jest użycie wzoru ze standardowym symbolem kapsla. Wprowadź następujące dane w komórkach arkusza roboczego:
| B | C | Formuła | Wynik | |
| 2 | 7 | 3 | =B2^C2 | 343 |
W ten sam sposób możesz podnieść żądaną wartość do dowolnej potęgi - ujemnej, ułamkowej. Zróbmy co następuje i odpowiedzmy na pytanie, jak podnieść liczbę do potęgi ujemnej. Przykład:
| B | C | Formuła | Wynik | |
| 2 | 7 | -3 | =B2^C2 | 0, 002915 |
Możesz poprawić=B2^-C2 bezpośrednio w formule.
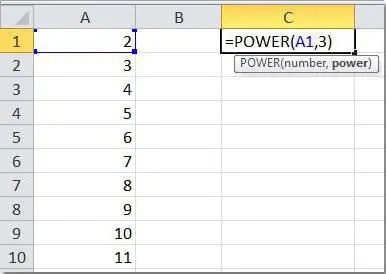
Drugą opcją jest użycie gotowej funkcji "Stopień", która przyjmuje dwa obowiązkowe argumenty - liczbę i wskaźnik. Aby zacząć z niego korzystać wystarczy w dowolnej wolnej komórce umieścić znak „równości” (=),wskazując na początek formuły i wprowadź powyższe słowa. Pozostaje wybrać dwie komórki, które będą uczestniczyć w operacji (lub ręcznie określić określone liczby) i nacisnąć klawisz Enter. Spójrzmy na kilka prostych przykładów.
| B | C | Formuła | Wynik | ||
| 2 | 7 | 3 | =MOC(B2;C2) | 343 | |
| 3 | 7 | -3 | =MOC(B3;C3) |
|
Jak widać, nie ma nic skomplikowanego w podnoszeniu liczby do potęgi ujemnej i do normalnej za pomocą programu Excel. W końcu, aby rozwiązać ten problem, możesz użyć zarówno znanego symbolu „pokrywy”, jak i łatwej do zapamiętania wbudowanej funkcji programu. To zdecydowany plus!
Przejdźmy do bardziej złożonych przykładów. Zapamiętajmy zasadę, jak podnieść liczbę do potęgi ujemnej znaku ułamkowego, a zobaczymy, że to zadanie jest bardzo łatwe do rozwiązania w programie Excel.
Wskaźniki ułamkowe
W skrócie, algorytm obliczania liczby z wykładnikiem ułamkowym jest następujący.
- Konwertuj ułamek na ułamek prawidłowy lub niewłaściwy.
- Podnieś naszą liczbę do licznika otrzymanego przekonwertowanego ułamka.
- Z liczby uzyskanej w poprzednim akapicie obliczyć pierwiastek, pod warunkiem, że wykładnik pierwiastkabędzie mianownikiem ułamka uzyskanego w pierwszym etapie.
Zgadzam się, że nawet podczas operowania małymi liczbami i właściwymi ułamkami takie obliczenia mogą zająć dużo czasu. Dobrze, że procesor arkusza kalkulacyjnego Excel nie dba o to, jaką liczbę i w jakim stopniu podnieść. Spróbuj rozwiązać następujący przykład w arkuszu programu Excel:
| B (liczba) | C | Konwertuj na ułamek | Formuła | Wynik | |
| 2 | 7 | 0, 4 | 2/5 | =MOC(B2;C2) | 2, 177906424 |
Korzystając z powyższych zasad, możesz sprawdzić i upewnić się, że obliczenia są poprawne.
Na końcu naszego artykułu, w formie tabeli ze wzorami i wynikami, podamy kilka przykładów, jak podnieść liczbę do potęgi ujemnej, a także kilka przykładów z liczbami ułamkowymi i potęgami.
Przykładowa tabela
Sprawdź następujące przykłady w arkuszu programu Excel. Aby wszystko działało poprawnie, podczas kopiowania formuły musisz użyć odwołania mieszanego. Ustal numer kolumny zawierającej podnoszony numer i numer wiersza zawierającego wskaźnik. Twoja formuła powinna wyglądać mniej więcej tak: „=$B4^C$3”.
| Numer / stopień | 1 | 2 | 3 | 0, 5 | -0, 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 1, 414214 | 0, 707107 |
| 7 | 7 | 49 | 343 | 2, 645751 | 0, 377964 |
| -7 | -7 | 49 | -343 | LICZBA! | LICZBA! |
| 0, 2 | 0, 2 | 0, 04 | 0, 008 | 0, 447214 | 2, 236068 |
| 0, 4 | 0, 4 | 0, 16 | 0, 064 | 0, 632456 |
1, 581139 |
| -0, 4 | -0, 4 | 0, 16 | -0, 064 | LICZBA! | LICZBA! |
Zauważ, że liczby dodatnie (nawet niecałkowite) są obliczane bez problemów dla jakichkolwiek wykładników. Nie ma problemów z podniesieniem dowolnych liczb do liczb całkowitych. Ale podniesienie liczby ujemnej do potęgi ułamkowej zamieni się w błąd, ponieważ nie można przestrzegać wskazanej zasadyna początku naszego artykułu o konstrukcji liczb ujemnych, ponieważ parzystość jest cechą wyłącznie liczby INTEGER.






