Piramida wraz z pryzmatem to doskonały wielościan w przestrzeni trójwymiarowej, ich cechy geometryczne badane są w liceum. W tym artykule zastanowimy się, czym są piramidy, z jakich elementów się składają, a także krótko scharakteryzujemy prawidłowe piramidy.
Piramida figur geometrycznych
Z punktu widzenia geometrii piramida jest figurą przestrzenną, składającą się z jednego wielokąta i kilku trójkątów. Uzyskanie tej liczby jest dość proste. Aby to zrobić, weź wielokąt o n bokach, a następnie wybierz dowolny punkt w przestrzeni, który nie będzie leżał w płaszczyźnie wielokąta i połącz każdy wierzchołek wielokąta z tym punktem. Oczywiście utworzona w ten sposób figura będzie miała n trójkątów połączonych ze sobą w jednym wierzchołku.
Aby zwizualizować geometryczny kształt opisywanej figury, zróbmy zdjęcie.

Pokazuje czworokątną piramidę, której podstawa jestczworoboczny, a powierzchnia boczna jest utworzona przez cztery trójkąty, które mają wspólny wierzchołek.
Elementy piramidy
Jak każdy wielościan, piramida składa się z trzech rodzajów elementów:
- krawędzie;
- topy;
- żeberka.
Twarze to części płaszczyzn, które oddzielają wewnętrzną objętość figury od otaczającej przestrzeni. Jeśli podstawa piramidy zawiera n-kąt, to liczba jej ścian wynosi zawsze n+1. Spośród nich n boków jest trójkątnych, a jedna strona to wspomniana podstawa n-kątna.
wierzchołki to punkty, w których przecinają się trzy lub więcej ścian figury. Region bazowy zawiera n wierzchołków, z których każdy składa się z dwóch trójkątnych ścian i podstawy. Punkt, w którym spotyka się n trójkątnych boków, nazywamy wierzchołkiem piramidy. Zatem rozważana figura składa się z n+1 wierzchołków.
Krawędzie to proste linie, które pojawiają się, gdy przecinają się dwie twarze. Każda krawędź jest ograniczona dwoma wierzchołkami na swoich końcach. Każda piramida o podstawie n-gon zawiera 2n krawędzi. Połowa tej liczby, czyli n, jest utworzona wyłącznie przez przecięcie bocznych trójkątów.
Możliwe rodzaje figur
Nazwa rozważanej figury jest jednoznacznie określona przez typ wielokąta u podstawy. Na przykład, jeśli ma trzy rogi i trzy boki, to piramida będzie trójkątna, jeśli cztery - czworokątna i tak dalej.
Wielokąt może być wypukły i wklęsły, a także regularny i ogólny. To wszystko determinuje również wygląd piramidy.
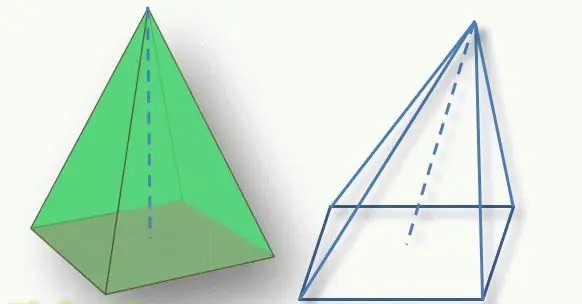
Ważnym punktem przy określaniu rodzaju figury jest położenie wierzchołka piramidy w stosunku do jej podstawy. Prostopadły odcinek narysowany od góry do podstawy wielokąta nazywany jest wysokością figury. Jeśli ten odcinek przecina podstawę w jej geometrycznym środku (dla trójkąta jest to przecięcie środkowych, dla czworokąta - przecięcie przekątnych), wówczas figurę nazywamy linią prostą. W przeciwnym razie mówią o nachylonej piramidzie.
Jeżeli n-kąt podstawy jest regularny (trójkąt równoboczny, kwadrat itp.), a figura jest prosta, to nazywamy ją piramidą regularną.
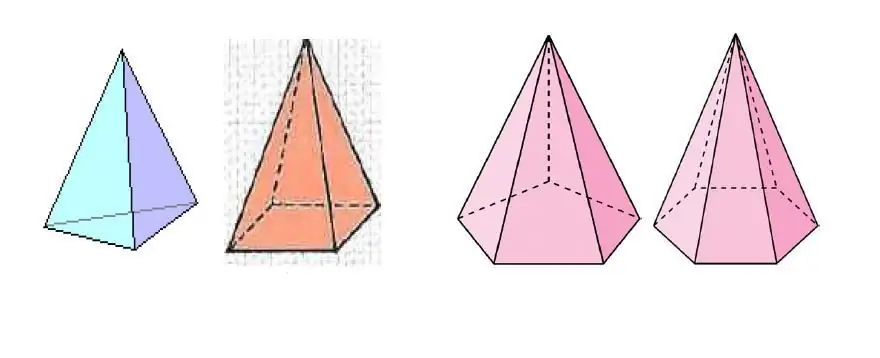
Powyższy rysunek przedstawia kilka piramid, które różnią się liczbą boków wielokąta u podstawy.
Właściwości regularnych piramid
Te piramidy różnią się od innych figur tej klasy wysokim stopniem symetrii. W związku z tym wygodnie jest przeprowadzać z nimi różne obliczenia geometryczne, na przykład objętość lub powierzchnię.
Regularna piramida zawiera u podstawy n-gon, którego powierzchnia jest jednoznacznie określona na podstawie wiedzy o długości jej boku. Boczną powierzchnię figury tworzy n identycznych trójkątów, które są równoboczne. Krawędzie regularnej piramidy znajdującej się na bocznej powierzchni są sobie równe. Wartość długości tej krawędzi jest często wykorzystywana przy obliczaniu twierdzenia figury i określaniu pola powierzchni.
Wysokość regularnej piramidy to druga ważna cecha figury (pierwsza to długość krawędzi)fusy). Wysokość jest używana podczas obliczania objętości.
Każda płaszczyzna równoległa do podstawy, która przecina boczne ściany piramidy, prowadzi do utworzenia przekroju wielokątnego. Jest jednorodny względem wielokąta bazowego. Opisana operacja plastra prowadzi do powstania całej klasy nowych figur - ściętych regularnych piramid.
Najsłynniejsze piramidy

Oczywiście są to regularne czworokątne piramidy egipskich faraonów. W miejscu zwanym Giza znajduje się ponad 100 tych kamiennych pomników, których doskonałość projektu i dokładność parametrów geometrycznych do dziś zadziwiają naukowców. Największą z nich jest Piramida Cheopsa, która ma około 146 metrów wysokości i około 230 metrów długości.
Do czego dokładnie służyły te piramidy, jakimi mechanizmami i kiedy zostały zbudowane, do dziś nikt nie wie.






