Istnieją obiekty, które są w stanie zmienić gęstość padającego na nie strumienia promieniowania elektromagnetycznego, to znaczy albo zwiększyć go przez zebranie go w jednym punkcie, albo zmniejszyć przez rozproszenie. Obiekty te nazywane są w fizyce soczewkami. Przyjrzyjmy się bliżej temu zagadnieniu.
Czym są soczewki w fizyce?
Ta koncepcja oznacza absolutnie każdy obiekt, który jest w stanie zmienić kierunek propagacji promieniowania elektromagnetycznego. Jest to ogólna definicja soczewek w fizyce, która obejmuje okulary optyczne, soczewki magnetyczne i grawitacyjne.
W tym artykule skupimy się na okularach optycznych, które są obiektami wykonanymi z przezroczystego materiału i ograniczonymi dwiema powierzchniami. Jedna z tych powierzchni musi koniecznie mieć krzywiznę (to znaczy być częścią kuli o skończonym promieniu), w przeciwnym razie obiekt nie będzie miał właściwości zmiany kierunku propagacji promieni świetlnych.
Zasada soczewki

Istota pracy tej nieskomplikowanejobiekt optyczny to zjawisko załamania promieni słonecznych. Na początku XVII wieku słynny holenderski fizyk i astronom Willebrord Snell van Rooyen opublikował prawo załamania, które obecnie nosi jego nazwisko. Sformułowanie tego prawa jest następujące: gdy światło słoneczne przechodzi przez granicę między dwoma optycznie przezroczystymi ośrodkami, to iloczyn sinusa kąta padania między wiązką a normalną do powierzchni oraz współczynnika załamania ośrodka, w którym propaguje jest wartością stałą.

Aby wyjaśnić powyższe, podajmy przykład: niech światło pada na powierzchnię wody, podczas gdy kąt między normalną do powierzchni a wiązką wynosi θ1. Następnie wiązka światła ulega załamaniu i zaczyna propagację w wodzie już pod kątem θ2 do normalnej do powierzchni. Zgodnie z prawem Snella otrzymujemy: sin(θ1)n1=sin(θ2) n2, gdzie n1 i n2 to współczynniki załamania dla powietrza i wody, odpowiednio. Jaki jest współczynnik załamania światła? Jest to wartość pokazująca, ile razy prędkość propagacji fal elektromagnetycznych w próżni jest większa niż dla ośrodka przezroczystego optycznie, czyli n=c/v, gdzie c i v to prędkości światła w próżni i w odpowiednio średnie.
Fizyka pojawiania się refrakcji polega na realizacji zasady Fermata, zgodnie z którą światło porusza się w taki sposób, aby w jak najkrótszym czasie pokonać odległość od jednego punktu do drugiego.
Rodzaje soczewek

Typ soczewki optycznej w fizyce jest określony wyłącznie przez kształt powierzchni, które ją tworzą. Od tego kształtu zależy kierunek załamania wiązki padającej na nie. Tak więc, jeśli krzywizna powierzchni jest dodatnia (wypukła), to po wyjściu z soczewki wiązka światła rozchodzi się bliżej jej osi optycznej (patrz niżej). I odwrotnie, jeśli krzywizna powierzchni jest ujemna (wklęsła), a następnie przechodząc przez szkło optyczne, wiązka odsunie się od swojej osi środkowej.
Zwróć uwagę, że powierzchnia o dowolnej krzywiźnie załamuje promienie w ten sam sposób (zgodnie z prawem Stelli), ale normalne do nich mają inne nachylenie w stosunku do osi optycznej, co skutkuje odmiennym zachowaniem załamanego promienia.
Soczewka ograniczona dwiema wypukłymi powierzchniami nazywana jest soczewką skupiającą. Z kolei jeśli tworzą go dwie powierzchnie o ujemnej krzywiźnie, nazywamy to rozpraszaniem. Wszystkie inne typy szkieł optycznych są związane z kombinacją tych powierzchni, do których dodaje się również płaszczyznę. Jakie właściwości będzie miała soczewka zespolona (rozbieżna lub zbieżna) zależy od całkowitej krzywizny promieni jej powierzchni.
Elementy soczewki i właściwości promieni

Aby wbudować soczewki w fizykę obrazu, musisz zapoznać się z elementami tego obiektu. Są one wymienione poniżej:
- Główna oś optyczna i środek. W pierwszym przypadku oznaczają linię prostą przechodzącą prostopadle do soczewki przez jej środek optyczny. Ten z kolei to punkt wewnątrz soczewki, przez który przechodzi wiązka nie ulega załamaniu.
- Ogniskowa i ogniskowa - odległość między środkiem a punktem na osi optycznej, który zbiera wszystkie promienie padające na soczewkę równolegle do tej osi. Ta definicja dotyczy kolekcjonowania okularów optycznych. W przypadku soczewek rozbieżnych to nie same promienie zbiegają się do punktu, ale ich urojona kontynuacja. Ten punkt nazywa się głównym celem.
- Moc optyczna. Jest to nazwa odwrotności ogniskowej, czyli D \u003d 1 / f. Mierzy się go w dioptriach (dioptriach), czyli 1 dioptrii.=1 m-1.
Oto główne właściwości promieni przechodzących przez soczewkę:
- wiązka przechodząca przez środek optyczny nie zmienia swojego kierunku ruchu;
- promienie padające równolegle do głównej osi optycznej zmieniają swój kierunek tak, że przechodzą przez główne ognisko;
- promienie padające na szkło optyczne pod dowolnym kątem, ale przechodzące przez jego ognisko, zmieniają swój kierunek propagacji w taki sposób, że stają się równoległe do głównej osi optycznej.
Powyższe właściwości promieni dla cienkich soczewek w fizyce (tak się je nazywa, ponieważ bez względu na to, jakie kule są uformowane i jak są grube, tylko właściwości optyczne obiektu mają znaczenie) są wykorzystywane do budowania w nich obrazów.
Obrazy w okularach optycznych: jak budować?
Poniżej znajduje się rysunek, który szczegółowo opisuje schematy konstruowania obrazów w soczewkach wypukłych i wklęsłych obiektu(czerwona strzałka) w zależności od położenia.
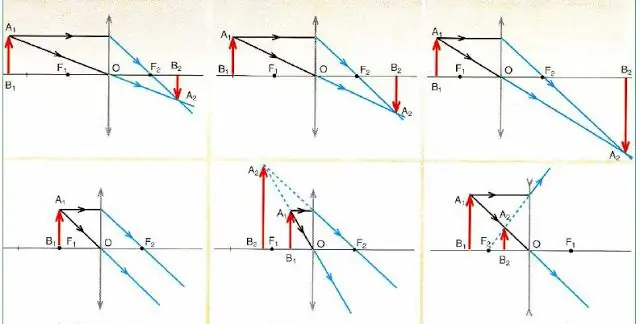
Ważne wnioski płyną z analizy obwodów na rysunku:
- Każdy obraz składa się tylko z 2 promieni (przechodzących przez środek i równoległych do głównej osi optycznej).
- Soczewki zbieżne (oznaczone strzałkami na końcach skierowanymi na zewnątrz) mogą dawać zarówno powiększony, jak i zmniejszony obraz, który z kolei może być rzeczywisty (rzeczywisty) lub wyimaginowany.
- Jeżeli obiekt jest ostry, soczewka nie tworzy swojego obrazu (patrz dolny diagram po lewej stronie na rysunku).
- Rozproszone okulary optyczne (oznaczone strzałkami na końcach skierowanymi do wewnątrz) zawsze dają zredukowany i wirtualny obraz, niezależnie od pozycji obiektu.
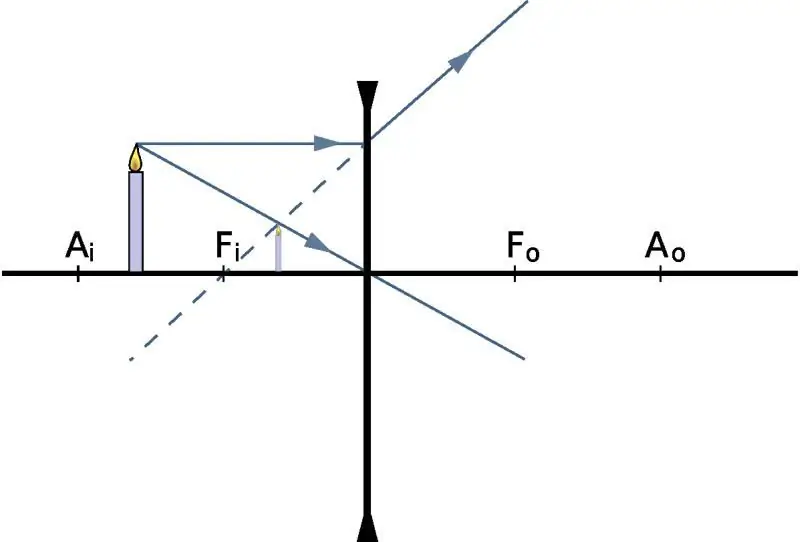
Znajdowanie odległości do obrazu
Aby określić, w jakiej odległości pojawi się obraz, znając położenie samego obiektu, podajemy wzór soczewki w fizyce: 1/f=1/do + 1 /d i, gdzie do i di są odległością do obiektu i jego obrazu od optycznego centrum, odpowiednio, f jest głównym ogniskiem. Jeśli mówimy o zbierającym szkle optycznym, to liczba f będzie dodatnia. I odwrotnie, dla soczewki rozbieżnej f jest ujemne.
Użyjmy tego wzoru i rozwiążmy prosty problem: niech obiekt będzie w odległości do=2f od środka zbierającego szkła optycznego. Gdzie pojawi się jego wizerunek?
Z warunku problemu mamy: 1/f=1/(2f)+1/di. Od: 1/di=1/f - 1/(2f)=1/(2f), tj. di=2 f. W ten sposób obraz pojawi się w odległości dwóch ognisk od obiektywu, ale po drugiej stronie niż sam obiekt (wskazuje na to znak dodatni o wartości di).
Krótka historia
Ciekawe jest podanie etymologii słowa „soczewka”. Pochodzi od łacińskich słów „soczewka” i „lentis”, co oznacza „soczewica”, ponieważ obiekty optyczne w swoim kształcie naprawdę wyglądają jak owoc tej rośliny.
Moc refrakcyjna sferycznych przezroczystych ciał była znana starożytnym Rzymianom. Użyli do tego celu okrągłych szklanych naczyń wypełnionych wodą. Same soczewki szklane zaczęto wytwarzać dopiero w XIII wieku w Europie. Były używane jako narzędzie do czytania (nowoczesne okulary lub szkło powiększające).
Aktywne wykorzystanie obiektów optycznych w produkcji teleskopów i mikroskopów sięga XVII wieku (na początku tego stulecia Galileusz wynalazł pierwszy teleskop). Zauważ, że matematyczne sformułowanie prawa załamania światła Stelli, bez wiedzy o którym niemożliwe jest wyprodukowanie soczewek o pożądanych właściwościach, zostało opublikowane przez holenderskiego naukowca na początku tego samego XVII wieku.
Inne soczewki
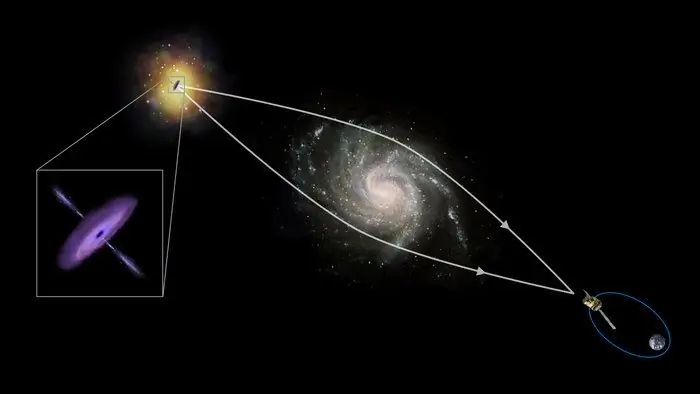
Jak wspomniano powyżej, oprócz optycznych obiektów refrakcyjnych istnieją również obiekty magnetyczne i grawitacyjne. Przykładem tych pierwszych są soczewki magnetyczne w mikroskopie elektronowym, żywym przykładem tych drugich jest zniekształcenie kierunku strumienia światła,kiedy przechodzi w pobliżu masywnych ciał kosmicznych (gwiazdy, planety).






