Moduł sprężystości to wielkość fizyczna, która charakteryzuje elastyczne zachowanie materiału po przyłożeniu do niego siły zewnętrznej w określonym kierunku. Zachowanie sprężyste materiału oznacza jego odkształcenie w obszarze sprężystym.
Historia badania elastyczności materiałów

Fizyczna teoria ciał sprężystych i ich zachowania pod wpływem sił zewnętrznych została szczegółowo przeanalizowana przez angielskiego naukowca z XIX wieku, Thomasa Younga. Jednak samo pojęcie sprężystości zostało opracowane już w 1727 r. przez szwajcarskiego matematyka, fizyka i filozofa Leonharda Eulera, a pierwsze eksperymenty związane z modułem sprężystości przeprowadzono w 1782 r., czyli 25 lat przed pracą Thomasa Junga., weneckiego matematyka i filozofa Jacopo Ricatti.
Zasługa Thomasa Younga polega na tym, że nadał teorii elastyczności smukły, nowoczesny wygląd, który został następnie sformalizowany w postaci prostego, a następnie uogólnionego prawa Hooke'a.
Fizyczny charakter elastyczności
Każde ciało składa się z atomów, pomiędzy którymi działają siły przyciągania i odpychania. Równowaga tych sił jeststan i parametry materii w danych warunkach. Atomy ciała stałego, gdy zostaną na nie przyłożone nieznaczne zewnętrzne siły rozciągające lub ściskające, zaczynają się przesuwać, tworząc siłę przeciwną do kierunku i równą wielkości, która ma tendencję do przywracania atomów do ich stanu początkowego.
W procesie takiego przemieszczania się atomów wzrasta energia całego układu. Eksperymenty pokazują, że przy małych odkształceniach energia jest proporcjonalna do kwadratu tych odkształceń. Oznacza to, że siła będąca pochodną po energii okazuje się być proporcjonalna do pierwszej potęgi odkształcenia, czyli zależy od niej liniowo. Odpowiadając na pytanie, jaki jest moduł sprężystości, możemy powiedzieć, że jest to współczynnik proporcjonalności między siłą działającą na atom a deformacją, którą ta siła powoduje. Wymiar modułu Younga jest taki sam jak wymiar ciśnienia (Pascal).
Elastyczny limit
Zgodnie z definicją, moduł sprężystości wskazuje, jak duże naprężenie musi być przyłożone do bryły, aby jej odkształcenie wyniosło 100%. Jednak wszystkie ciała stałe mają granicę sprężystości równą 1% odkształcenia. Oznacza to, że jeśli przyłożona zostanie odpowiednia siła i ciało odkształci się o mniej niż 1%, to po odstawieniu tej siły ciało dokładnie odzyskuje swój pierwotny kształt i wymiary. W przypadku przyłożenia zbyt dużej siły, przy której wartość odkształcenia przekroczy 1%, po zakończeniu działania siły zewnętrznej ciało nie będzie już przywracać swoich pierwotnych wymiarów. W tym drugim przypadku mówi się o istnieniu deformacji szczątkowej, która jestdowód na przekroczenie granicy elastyczności materiału.
Moduł Younga w akcji
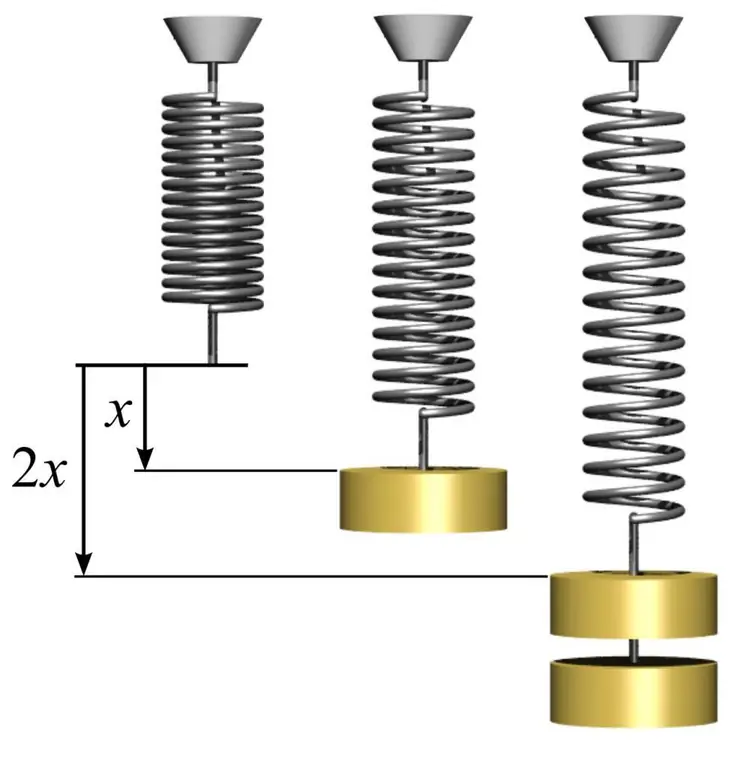
Aby określić moduł sprężystości, a także zrozumieć, jak go używać, możesz podać prosty przykład ze sprężyną. Aby to zrobić, musisz wziąć metalową sprężynę i zmierzyć powierzchnię koła, z którego tworzą się jej cewki. Odbywa się to za pomocą prostego wzoru S=πr², gdzie n to pi równe 3,14, a r to promień zwoju sprężyny.
Następnie zmierz długość sprężyny l0 bez obciążenia. Jeżeli zawiesisz na sprężynie jakieś obciążenie o masie m1, to zwiększy ono jego długość do określonej wartości l1. Moduł sprężystości E można obliczyć znając prawo Hooke'a ze wzoru: E=m1gl0/(S(l 1-l0)), gdzie g jest przyspieszeniem swobodnego spadania. W tym przypadku zauważamy, że wielkość odkształcenia sprężyny w obszarze elastycznym może znacznie przekroczyć 1%.
Znajomość modułu Younga pozwala przewidzieć wielkość odkształcenia pod działaniem określonego naprężenia. W tym przypadku, jeśli zawiesimy kolejną masę m2 na sprężynie, otrzymamy następującą wartość odkształcenia względnego: d=m2g/ (SE), gdzie d - względne odkształcenie w obszarze sprężystym.
Izotropia i anizotropia
Moduł sprężystości jest cechą materiału, która opisuje siłę wiązania między jego atomami i cząsteczkami, jednak konkretny materiał może mieć kilka różnych modułów Younga.
Faktem jest, że właściwości każdej bryły zależą od jej wewnętrznej struktury. Jeśli właściwości są takie same we wszystkich kierunkach przestrzennych, mówimy o materiale izotropowym. Takie substancje mają jednorodną strukturę, więc działanie na nie siły zewnętrznej w różnych kierunkach powoduje taką samą reakcję materiału. Wszystkie materiały amorficzne, takie jak guma czy szkło, są izotropowe.
Anizotropia to zjawisko, które charakteryzuje się zależnością właściwości fizycznych ciała stałego lub cieczy od kierunku. Wszystkie metale i stopy na nich oparte mają taką lub inną sieć krystaliczną, czyli uporządkowany, a nie chaotyczny układ rdzeni jonowych. Dla takich materiałów moduł sprężystości zmienia się w zależności od osi działania naprężenia zewnętrznego. Na przykład metale o symetrii sześciennej, takie jak aluminium, miedź, srebro, metale ogniotrwałe i inne, mają trzy różne moduły Younga.
Moduł ścinania
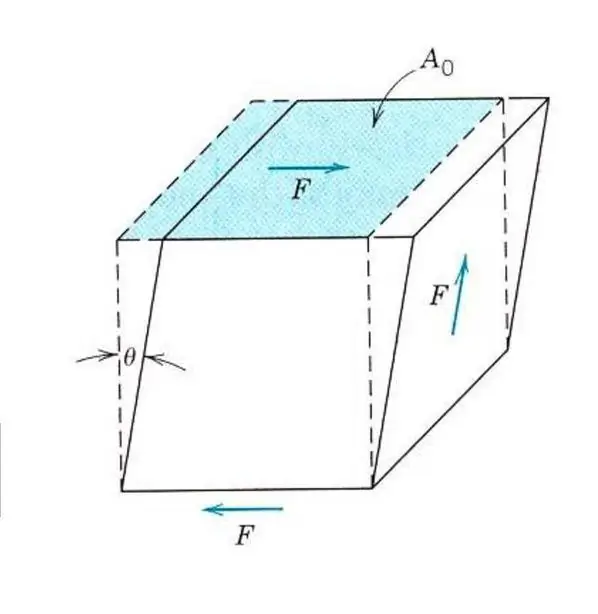
Opisanie właściwości sprężystych nawet materiału izotropowego nie wymaga znajomości jednego modułu Younga. Ponieważ oprócz rozciągania i ściskania na materiał mogą wpływać naprężenia ścinające lub naprężenia skręcające. W takim przypadku inaczej zareaguje na siłę zewnętrzną. Aby opisać odkształcenie sprężyste przy ścinaniu, wprowadzono analogię modułu Younga, modułu ścinania lub modułu sprężystości drugiego rodzaju.
Wszystkie materiały wytrzymują naprężenia ścinające mniej niż rozciąganie lub ściskanie, więc wartość modułu ścinania dla nich jest 2-3 razy mniejsza niż wartość modułu Younga. Zatem dla tytanu, którego moduł Younga jest równy 107 GPa, moduł sprężystości poprzecznej wynositylko 40 GPa, dla stali liczby te wynoszą odpowiednio 210 GPa i 80 GPa.
Moduł sprężystości drewna

Drewno jest materiałem anizotropowym, ponieważ włókna drewna są ułożone w określonym kierunku. To wzdłuż włókien mierzy się moduł sprężystości drewna, ponieważ jest on o 1-2 rzędy wielkości mniejszy w poprzek włókien. Znajomość modułu Younga dla drewna jest ważna i brana pod uwagę przy projektowaniu konstrukcji z płyt drewnianych.
Wartości modułu sprężystości drewna dla niektórych rodzajów drzew przedstawiono w poniższej tabeli.
| Widok drzewa | Moduł Younga w GPa |
| Drzewo laurowe | 14 |
| Eukaliptus | 18 |
| Cedr | 8 |
| Świerk | 11 |
| Sosna | 10 |
| Dąb | 12 |
Należy zauważyć, że podane wartości mogą różnić się nawet o 1 GPa dla konkretnego drzewa, ponieważ na jego moduł Younga ma wpływ gęstość drewna i warunki wzrostu.

Moduły ścinania dla różnych gatunków drzew mieszczą się w przedziale 1-2 GPa, np. dla sosny to 1,21 GPa, a dla dębu 1,38 GPa, czyli drewno praktycznie nie wytrzymuje naprężeń ścinających. Fakt ten należy wziąć pod uwagę przy wytwarzaniu drewnianych konstrukcji nośnych, które są przeznaczone do pracy wyłącznie przy rozciąganiu lub ściskaniu.
Elastyczne właściwości metali
W porównaniu z modułem Younga drewna, średnie wartości tej wartości dla metali i stopów są o rząd wielkości większe, jak pokazano w poniższej tabeli.
| Metal | Moduł Younga w GPa |
| Brązowy | 120 |
| Miedź | 110 |
| Stal | 210 |
| Tytan | 107 |
| Nikiel | 204 |
Elastyczne właściwości metali o sześciennej syngonii są opisane przez trzy stałe sprężystości. Do takich metali należą miedź, nikiel, aluminium, żelazo. Jeśli metal ma heksagonalną syngonię, do opisania jego właściwości sprężystych potrzeba już sześciu stałych.
W przypadku systemów metalicznych moduł Younga jest mierzony w granicach 0,2% odkształcenia, ponieważ duże wartości mogą już występować w obszarze niesprężystym.






