W fizyce badany jest temat połączeń równoległych i szeregowych, i mogą to być nie tylko przewodniki, ale także kondensatory. Ważne jest, aby nie pomylić się z tym, jak każdy z nich wygląda na schemacie. I dopiero wtedy zastosuj określone formuły. Przy okazji, trzeba je zapamiętać na pamięć.
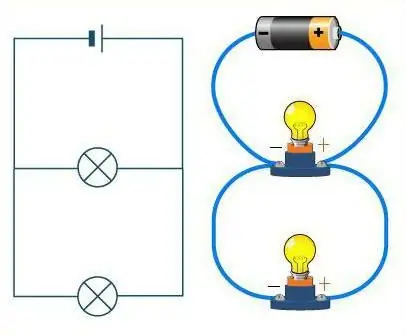
Jak odróżnić te dwa związki?
Przyjrzyj się bliżej diagramowi. Jeśli przewody są reprezentowane jako droga, samochody na niej będą odgrywać rolę rezystorów. Na prostej drodze bez rozwidlenia samochody jadą jeden za drugim, po łańcuchu. Podobnie wygląda szeregowe połączenie przewodów. Droga w tym przypadku może mieć nieograniczoną liczbę zakrętów, ale nie pojedyncze skrzyżowanie. Bez względu na to, jak potoczy się droga (przewody), maszyny (oporniki) zawsze będą ulokowane jedna po drugiej, w jednym łańcuchu.
To zupełnie inna sprawa, jeśli rozważane jest połączenie równoległe. Wtedy rezystory można porównać z atletami na starcie. Oni sąkażdy stoi na swoim torze, ale mają ten sam kierunek ruchu, a linia mety jest w tym samym miejscu. Podobnie rezystory - każdy z nich ma swój własny przewód, ale wszystkie są w pewnym momencie połączone.
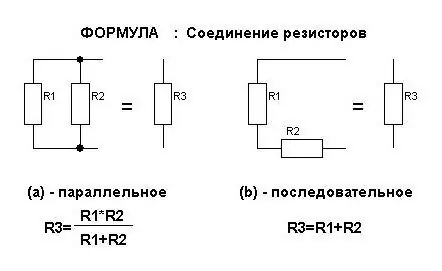
Formuły dla aktualnej siły
Zawsze jest to omawiane w temacie „Elektryczność”. Połączenia równoległe i szeregowe wpływają na wielkość prądu w rezystorach w różny sposób. Dla nich wyprowadzane są formuły, które można zapamiętać. Ale wystarczy tylko zapamiętać znaczenie, jakie jest w nich zainwestowane.
Więc prąd w szeregowym połączeniu przewodów jest zawsze taki sam. Oznacza to, że w każdym z nich wartość aktualnej siły nie jest inna. Możesz narysować analogię, porównując drut z rurą. W nim woda płynie zawsze w ten sam sposób. I wszystkie przeszkody na jego drodze zostaną zmiecione z tą samą siłą. To samo z prądem. Dlatego wzór na całkowity prąd w obwodzie z szeregowym połączeniem rezystorów wygląda następująco:
I gen=I 1=I 2
Tutaj litera I oznacza siłę prądu. Jest to powszechna notacja, więc musisz ją zapamiętać.
Prąd w połączeniu równoległym nie będzie już wartością stałą. Z tej samej analogii z rurą okazuje się, że woda zostanie podzielona na dwa strumienie, jeśli główna rura ma odgałęzienie. To samo zjawisko obserwuje się przy prądzie, gdy na jego drodze pojawia się rozgałęzienie przewodów. Wzór na całkowitą siłę prądu, gdy przewody są połączone równolegle:
I gen=I 1 + I 2
Jeśli rozgałęzienie składa się z przewodów, którewięcej niż dwa, to w powyższym wzorze będzie więcej wyrazów o tej samej liczbie.
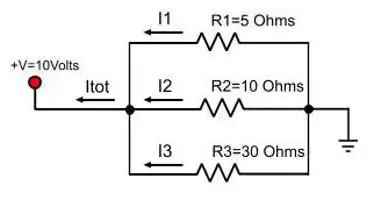
Formuły na stres
Gdy rozważany jest obwód, w którym przewody są połączone szeregowo, napięcie w całej sekcji jest określane przez sumę tych wartości na każdym konkretnym rezystorze. Możesz porównać tę sytuację z płytami. Jedna osoba będzie mogła łatwo utrzymać jedną z nich, druga będzie mogła również wziąć w pobliżu, ale z trudem. Jedna osoba nie będzie już w stanie utrzymać trzech talerzy obok siebie, potrzebna będzie pomoc drugiej. Itp. Wysiłki ludzi się sumują.
Wzór na całkowite napięcie odcinka obwodu z szeregowym połączeniem przewodów wygląda następująco:
U gen=U 1 + U 2, gdzie U jest przyjętym oznaczeniem dla napięcia elektrycznego.
Inna sytuacja powstaje, gdy rozważane jest równoległe połączenie rezystorów. Gdy talerze są ułożone jeden na drugim, nadal może je trzymać jedna osoba. Więc nie musisz nic dodawać. Tę samą analogię obserwuje się, gdy przewody są połączone równolegle. Napięcie na każdym z nich jest takie samo i równe temu, które jest na wszystkich naraz. Wzór na napięcie całkowite to:
U gen=U 1=U 2
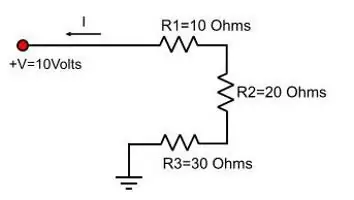
Wzory na opór elektryczny
Nie możesz ich już zapamiętywać, ale znać formułę prawa Ohma i wywnioskować z niego pożądane. Z tego prawa wynika, żenapięcie jest równe iloczynowi prądu i oporu. Oznacza to, że U=IR, gdzie R jest oporem.
Wtedy wzór, z którym będziesz musiał pracować, zależy od sposobu podłączenia przewodów:
- w szeregu, więc potrzebujesz równości napięcia - IgenRtotal=I1R1 + I2R2;
- równolegle konieczne jest użycie wzoru na aktualną siłę - Utotal / Rtotal=U 1/ R1 + U2 / R2 .
Po nich następują proste przekształcenia, które polegają na tym, że w pierwszej równości wszystkie prądy mają tę samą wartość, a w drugiej napięcia są równe. Więc można je skrócić. Oznacza to, że uzyskuje się następujące wyrażenia:
- R gen=R 1 + R 2 (dla szeregowego połączenia przewodów)
- 1 / R gen=1 / R 1 + 1 / R 2(przy połączeniu równoległym).
Gdy liczba rezystorów podłączonych do sieci wzrasta, zmienia się liczba terminów w tych wyrażeniach.
Warto zauważyć, że równoległe i szeregowe połączenie przewodów ma inny wpływ na całkowitą rezystancję. Pierwszy z nich zmniejsza rezystancję odcinka obwodu. Co więcej, okazuje się, że jest mniejszy niż najmniejszy z zastosowanych rezystorów. Po połączeniu szeregowym wszystko jest logiczne: wartości sumują się, więc łączna liczba zawsze będzie największa.
Prąd pracy
Poprzednie trzy wielkości składają się na prawa połączenia równoległego i szeregowego układu przewodów w obwodzie. Dlatego konieczne jest ich poznanie. Jeśli chodzi o pracę i moc, wystarczy pamiętać o podstawowej formule. Jest napisane w następujący sposób: A \u003d IUt, gdzie A jest pracą prądu, t jest czasem jego przejścia przez przewodnik.
Aby określić całkowitą pracę z połączeniem szeregowym, musisz wymienić napięcie w oryginalnym wyrażeniu. Otrzymujesz równość: A \u003d I(U 1 + U 2)t, otwierając nawiasy, w których okazuje się, że praca na całej sekcji jest równa ich ilości na każdym konkretnym bieżącym odbiorcy.
Rozumowanie przebiega podobnie, jeśli rozważany jest schemat połączenia równoległego. Tylko aktualna siła ma zostać zastąpiona. Ale wynik będzie taki sam: A=A 1 + A 2.
Aktualna moc
Wyprowadzając wzór na moc (zapis „P”) odcinka obwodu, ponownie musisz użyć jednego wzoru: P \u003d UI. Po takim rozumowaniu okazuje się, że połączenia równoległe i szeregowe są opisany takim wzorem na moc: P \u003d P1 + P 2.
Oznacza to, że niezależnie od tego, jak zostaną opracowane schematy, całkowita władza będzie sumą osób zaangażowanych w pracę. To tłumaczy fakt, że w sieci mieszkania nie da się jednocześnie włączyć wielu wydajnych urządzeń. Ona po prostu nie może znieść ciężaru.
Jak podłączenie przewodów wpływa na naprawę girlandy noworocznej?
Zaraz po przepaleniu się jednej z żarówek staje się jasne, w jaki sposób zostały połączone. Na połączenie szeregowe, żaden z nich się nie zapali. Wynika to z faktu, że lampa, która stała się bezużyteczna, powoduje przerwę w obwodzie. Dlatego musisz wszystko sprawdzić, aby ustalić, który jest wypalony, wymień go - a girlanda zacznie działać.
Jeśli używa połączenia równoległego, nie przestanie działać, jeśli jedna z żarówek przestanie działać. W końcu łańcuch nie zostanie całkowicie zerwany, ale tylko jedna równoległa część. Aby naprawić taką girlandę, nie trzeba sprawdzać wszystkich elementów obwodu, a jedynie te, które nie świecą.
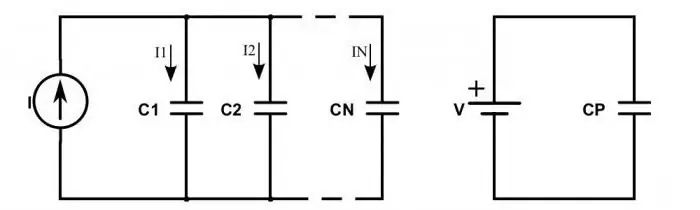
Co stanie się z obwodem, jeśli zamiast rezystorów zostaną zastosowane kondensatory?
Gdy są one połączone szeregowo, obserwuje się następującą sytuację: ładunki z plusów źródła zasilania docierają tylko do zewnętrznych płytek skrajnych kondensatorów. Ci pomiędzy po prostu przekazują ten ładunek wzdłuż łańcucha. To wyjaśnia fakt, że na wszystkich tabliczkach pojawiają się te same ładunki, ale z różnymi znakami. Dlatego ładunek elektryczny każdego kondensatora połączonego szeregowo można zapisać w następujący sposób:
q gen =q 1=q 2.
Aby określić napięcie na każdym kondensatorze, musisz znać wzór: U=q / C. W nim C jest pojemnością kondensatora.
Całkowite napięcie jest zgodne z tym samym prawem co rezystory. Dlatego zastępując napięcie we wzorze na pojemność sumą otrzymujemy, że całkowitą pojemność urządzeń należy obliczyć ze wzoru:
C=q / (U 1 + U2).
Możesz uprościć ten wzór, odwracając ułamki i zastępując stosunek napięcia do ładunku pojemnością. Okazuje się następująca równość: 1 / С=1 / С 1 + 1 / С 2.
Sytuacja wygląda nieco inaczej, gdy kondensatory są połączone równolegle. Wtedy całkowity ładunek jest określany przez sumę wszystkich ładunków, które gromadzą się na płytkach wszystkich urządzeń. A wartość napięcia jest nadal określana zgodnie z ogólnymi prawami. Dlatego wzór na całkowitą pojemność kondensatorów połączonych równolegle jest następujący:
С=(q 1 + q 2) / U.
Oznacza to, że ta wartość jest traktowana jako suma każdego z urządzeń używanych w połączeniu:
S=S 1 + S 2.
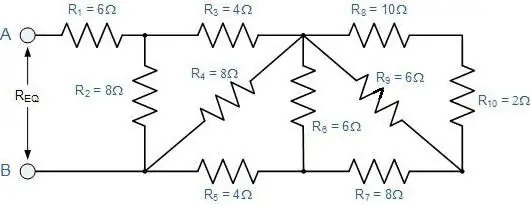
Jak określić całkowitą rezystancję dowolnego połączenia przewodów?
To jest taki, w którym kolejne sekcje zastępują sekcje równoległe i na odwrót. Dla nich wszystkie opisane prawa są nadal aktualne. Wystarczy, że zastosujesz je etapami.
Po pierwsze, ma to na celu mentalne rozwinięcie schematu. Jeśli trudno to sobie wyobrazić, musisz narysować, co się dzieje. Wyjaśnienie stanie się jaśniejsze, jeśli rozważymy je na konkretnym przykładzie (patrz rysunek).
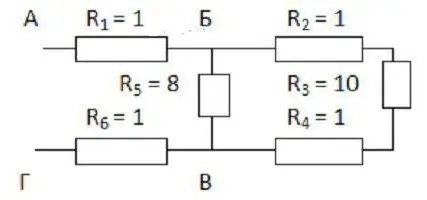
Wygodnie jest zacząć rysować od punktów B i C. Muszą one być umieszczone w pewnej odległości od siebie i od krawędzi arkusza. Po lewej jeden przewód zbliża się do punktu B, a dwa są już skierowane w prawo. Z drugiej strony punkt B ma dwie gałęzie po lewej stronie i jeden przewód za nim.
Teraz musisz wypełnić przestrzeń między nimikropki. Wzdłuż górnego przewodu należy umieścić trzy rezystory o współczynnikach 2, 3 i 4, a od dołu ten o indeksie 5. Pierwsze trzy są połączone szeregowo. Z piątym rezystorem są one równoległe.
Pozostałe dwa rezystory (pierwszy i szósty) są połączone szeregowo z rozważaną sekcją BV. Dlatego rysunek można po prostu uzupełnić dwoma prostokątami po obu stronach wybranych punktów. Pozostaje zastosować wzory do obliczania oporu:
- pierwszy podany dla połączenia szeregowego;
- następnie dla równoległego;
- i znowu dla kolejnych.
W ten sposób możesz wdrożyć dowolny, nawet bardzo złożony schemat.
Problem szeregowego połączenia przewodów
Warunek. Dwie lampy i rezystor są połączone w obwód jedna za drugą. Całkowite napięcie wynosi 110 V, a prąd 12 A. Jaka jest wartość rezystora, jeśli każda lampa ma znamionową wartość 40 V?
Decyzja. Ponieważ rozważane jest połączenie szeregowe, znane są wzory na jego prawa. Wystarczy je poprawnie zastosować. Zacznij od ustalenia wartości napięcia na rezystorze. Aby to zrobić, musisz od sumy odjąć dwa razy napięcie jednej lampy. Okazuje się, że 30 V.
Teraz, gdy znane są dwie wielkości, U i I (druga z nich jest podana w warunku, ponieważ całkowity prąd jest równy prądowi każdego odbiornika szeregowego), możemy obliczyć rezystancję rezystora za pomocą Prawo Ohma. Okazuje się, że to 2,5 oma.
Odpowiedź. Rezystancja rezystora wynosi 2,5 oma.
Zadaniedo podłączenia kondensatorów, równoległych i szeregowych
Warunek. Istnieją trzy kondensatory o pojemności 20, 25 i 30 mikrofaradów. Określ ich całkowitą pojemność po połączeniu szeregowym i równoległym.
Decyzja. Łatwiej jest zacząć od połączenia równoległego. W tej sytuacji wszystkie trzy wartości wystarczy dodać. Zatem całkowita pojemność wynosi 75uF.
Obliczenia będą nieco bardziej skomplikowane, gdy te kondensatory zostaną połączone szeregowo. W końcu najpierw musisz znaleźć stosunek jedności do każdej z tych zdolności, a następnie dodać je do siebie. Okazuje się, że jednostka podzielona przez łączną wydajność to 37/300. Wtedy pożądana wartość wynosi około 8 mikrofaradów.
Odpowiedź. Całkowita pojemność w połączeniu szeregowym wynosi 8 uF, równolegle - 75 uF.






